How Many Earthquake Records to Use for Design
Abstract
The analysis of structures is a fundamental part of seismic design and assessment. It began more than a 100 years ago, when static analysis with lateral loads of about 10% of the weight of the structure was adopted in seismic regulations. For a long time seismic loads of this size remained in the majority of seismic codes worldwide. In the course of time, more advanced analysis procedures were implemented, taking into account the dynamics and nonlinear response of structures. In the future methods with explicit probabilistic considerations may be adopted as an option. In this paper, the development of seismic provisions as related to analysis is summarized, the present state is discussed, and possible further developments are envisaged.
Introduction: as simple as possible but not simpler
Seismic analysis is a tool for the estimation of structural response in the process of designing earthquake resistant structures and/or retrofitting vulnerable existing structures. In principle, the problem is difficult because the structural response to strong earthquakes is dynamic, nonlinear and random. All three characteristics are unusual in structural engineering, where the great majority of problems are (or at least can be adequately approximated as) static, linear and deterministic. Consequently, special skills and data are needed for seismic design, which an average designer does not necessarily have.
Methods for seismic analysis, intended for practical applications, are provided in seismic codes. (Note that in this paper the term "code" is used broadly to include codes, standards, guidelines, and specifications.) Whereas the most advanced analytical, numerical and experimental methods should be used in research aimed at the development of new knowledge, the methods used in codes should, as Albert Einstein said, be "as simple as possible, but not simpler". A balance between required accuracy and complexity of analysis should be found, depending on the importance of a structure and on the aim of the analysis. It should not be forgotten that the details of the ground motion during future earthquakes are unpredictable, whereas the details of the dynamic structural response, especially in the inelastic range, are highly uncertain. According to Aristotle, "it is the mark of an educated mind to rest satisfied with the degree of precision which the nature of the subject admits and not to seek exactness where only an approximation is possible" (Nicomachean Ethics, Book One, Chapter 3).
After computers became widely available, i.e. in the late 1960s and in 1970s, a rapid development of procedures for seismic analysis and supporting software was witnessed. Nowadays, due to tremendous development in computing power, numerical methods, and software, there are almost no limits related to computation. Unfortunately, knowledge about ground motion and structural behaviour, especially in the inelastic range, has not kept up the same speed. Also, we cannot expect that, in general, the basic capabilities of engineers will be better than in the past. So, there is a danger, as M. Sozen wrote already in 2002: "Today, ready access to versatile and powerful software enables the engineer to do more and think less." (M. Sozen, A Way of Thinking, EERI Newsletter, April 2002.) Two other giants in earthquake engineering also made observations which have remained valid up to now. R. Clough, one of the fathers of the finite element method, stated: "Depending on the validity of the assumptions made in reducing the physical problem to a numerical algorithm, the computer output may provide a detailed picture of the true physical behavior or it may not even remotely resemble it" (Clough 1980, p. 369). Bertero (2009, p. 80) warned: "There are some negative aspects to the reliance on computers that we should be concerned about. It is unfortunate that there has been a trend among the young practicing engineers who are conducting structural analysis, design, and detailing using computers to think that the computer automatically provides reliability". Today it is lack of reliable data and the limited capabilities of designers which represent the weak link in the chain representing the design process, rather than computational tools, as was the case in the past.
An indication of the restricted ability of the profession (on average) to adequately predict the seismic structural response was presented by the results of a blind prediction contest of a simple full-scale reinforced concrete bridge column with a concentrated mass at the top, subjected to six consecutive unidirectional ground motions. A description of the contest, and of the results obtained, described in the following text, has been summarized from Terzic et al. (2015). The column was not straightened or repaired between the tests. During the first ground motion, the column displaced within its elastic range. The second test initiated a nonlinear response of the column, whereas significant nonlinearity of the column response was observed during the third test. Each contestant/team had to predict peak response for global (displacement, acceleration, and residual displacement), intermediate (bending moment, shear, and axial force), and local (axial strain and curvature) response quantities for each earthquake. Predictions were submitted by 41 teams from 14 different countries. The contestants had either MSc or PhD degrees. They were supplied with data about the ground motions and structural details, including the complete dimensions of the test specimen, and the mechanical one-dimensional properties of the steel and concrete. In this way the largest sources of uncertainties, i.e. the characteristics of the ground motion and the material characteristics, were eliminated. The only remaining uncertainty was related to the modelling and analysis of the structural response. In spite of this fact, the results showed a very wide scatter in the blind predictions of the basic engineering response parameters. For example, the average coefficient of variation in predicting the maximum displacement and acceleration over the six ground motions was 39 and 48%, respectively. Biases in median predicted responses were significant, varying for the different tests from 5 to 35% for displacement, and from 25 to 118% for acceleration. More detailed results for the maximum displacements at the top of the column and the maximum shear forces at the base of the column are presented in Fig. 1. A large dispersion of the results can be observed even in the case of the elastic (Eq. 1) and nearly elastic (Eq. 2) structural behaviour.
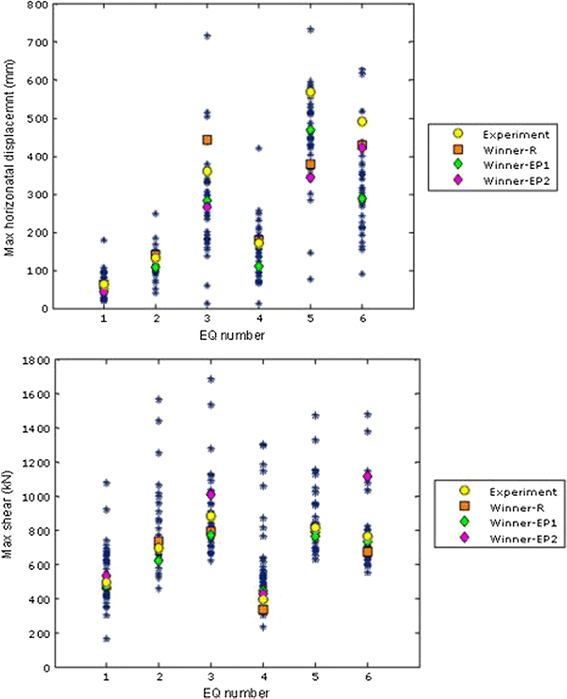
Predictions of maximum horizontal displacements at the top of the column and maximum base shears versus measured values (Terzic et al. 2015)
Full size image
The results of the blind prediction contest clearly demonstrate that the most advanced and sophisticated models and methods do not necessarily lead to adequate results. For example, it was observed that a comparable level of accuracy could be achieved if the column was modelled either with complex force-based fibre beam-column elements or with simpler beam-column elements with concentrated plastic hinges. Predictions of structural response greatly depended on the analyst's experience and modelling skills. Some of the results were completely invalid and could lead to gross errors if used in design. A simple check, e.g. with the response spectrum approach applied for a single-degree-of-freedom system, would indicate that the results were nonsensical.
This paper deals with analysis procedures used in seismic provisions. The development of seismic provisions related to the analysis of building structures is summarized, the present state is discussed, and possible further developments are envisaged. Although, in general, the situation in the whole world is discussed, in some cases emphasis is placed on the situation in Europe and on the European standard for the design of structures for earthquake resistance Eurocode 8 (CEN 2004), denoted in this paper as EC8. The discussion represents the views of the author and is based on his experience in teaching, research, consulting, and code development work.
History: domination of the equivalent static procedure and introduction of dynamics
Introduction
Earthquake engineering is a relatively young discipline, "it is a twentieth century development" (Housner 1984). Although some types of old buildings have, for centuries, proved remarkably resistant to earthquake forces, their seismic resistance has been achieved by good conceptual design without any seismic analysis. Early provisions related to the earthquake resistance of buildings, e.g. in Lima, Peru (Krause 2014) and Lisbon, Portugal (Cardoso et al. 2004), which were adopted after the disastrous earthquakes of 1699 and 1755, respectively, were restricted to construction rules and height limitations. It appears that the first engineering recommendations for seismic analysis were made in 1909 in Italy. Apparently Housner considered this date as the starting date of Earthquake Engineering.
The period up to 1978 was dominated by the equivalent static procedure. "The equivalent static method gradually spread to seismic countries around the world. First it was used by progressive engineers and later was adopted by building codes. Until the 1940s it was the standard method of design required by building codes" (Housner 1984), and still today it is widely used for simple regular structures, with updated values for the seismic coefficients. "This basic method has stood the test of time as an adequate way to proportion the earthquake resistance of most buildings. Better methods would evolve, but the development of an adequate seismic force analysis method stands out in history as the first major saltation or jump in the state of the art." (Reitherman 2012, p. 174). From the three basic features of seismic structural response, dynamics was the first to be introduced. Later, inelastic behaviour was approximately taken into account by the gradation of seismic loads for different structural systems, whereas randomness was considered implicitly by using various safety factors.
In the following sections we will summarize the development of seismic analysis procedures in different codes (see also Table 1). It will be shown that, initially, the equivalent static approach was used. With some exceptions, for several decades the seismic coefficient mostly amounted to about 0.1.
Full size table
Dynamic considerations were introduced by relating the seismic coefficient to the period of the building, indirectly via the number of storeys in 1943, and directly in 1956. The modal response spectrum method appeared for the first time in 1957. The impact of the energy dissipation capacity of structures in the inelastic range (although this was not explicitly stated in the code) was taken into account in 1959. Modern codes can be considered to have begun with the ATC 3-06 document "Tentative provisions for the development of seismic regulations for buildings", which was released in 1978 (ATC 1978). This document formed the basis upon which most of the subsequent guidelines and regulations were developed both in the United States and elsewhere in the world.
When discussing seismic code developments, the capacity design approach developed in the early 1970s in New Zealand, should not be ignored. It might be one of the most ingenious solutions in earthquake engineering. Structures designed by means of the capacity design approach are expected to possess adequate ductility both at the local and global level. In the case of such structures, it is completely legitimate to apply linear analysis with a force reduction factor which takes into account the energy dissipation capacity. Of course, a quantification of the inelastic behaviour is not possible. Since capacity design is not a direct part of the analysis process, it will not be further discussed in this paper.
Italy
After the earthquake in Messina in 1908, a committee of Italian experts (nine practicing engineers and five university professors) was formed. The committee prepared a quantitative recommendation for seismic analysis which was published in 1909. The committee proposed, mainly based on the results of a study of three timber-framed buildings which had survived the earthquake with little or no damage, that, "in future, structures must be so designed that they would resist, in the first story, a horizontal force equivalent to 1/12th of the weight above, and in the second and third story, 1/8th of the weight above" (Freeman 1932, p. 577). The procedure became mandatory through a Royal Decree in the same year (Sorrentino 2007). At that time, three-story buildings were the tallest permitted. In the committee report it was stated "that it was reasonable to add 50% to the seismic force to be provided against in upper stories, because of the observed greater amplitude of oscillation in tall as compared with low buildings and also in adherence to the universally admitted principle that the center of gravity of buildings should be as low as possible, and hence the upper stories should be lighter than the lower" (Freeman 1932, p. 577). According to Reitherman (2012, p. 193), the above-described technical regulation was later adjusted to provide factors of 1/8 and 1/6, respectively, after the disastrous 1915 Avezzano Earthquake, to the north of the Strait of Messina.
The committee's proposal for the determination of lateral forces actually introduced the seismic coefficient, which is used to multiply the weight of the building in order to obtain the total seismic force (the base shear force). The seismic coefficient enables performing a seismic analysis by means of the equivalent static method. It has a theoretical basis. According to D'Alembert's principle, a fictitious inertia force, proportional to the acceleration and mass of a particle, and acting in the direction opposite to the acceleration, can be used in a static analysis, in order to simulate a dynamic problem. The seismic coefficient represents the ratio between the acceleration of the mass and the acceleration of gravity. The acceleration of the mass depends on the acceleration of the ground and on the dynamic characteristics of the structure. At the beginning of the twentieth century there were no data about ground accelerations and the use of structural dynamics was, at that time, therefore infeasible. M. Panetti, who appears to be the main author of the recommendation of seismic coefficient in the report after the Messina earthquake, recognized "that the problem was really one of dynamics or kinetics, and that to solve this would involve such complication that one must have recourse to the assumption that a problem of statics could be so framed as to provide for safety" (Freeman 1932, p. 577). So, according to Freeman, the proposed seismic coefficient, as well as the seismic coefficients used during the following decades in California and Japan, were "largely a guess tempered by judgement". Nevertheless, it is interesting to note that the order of magnitude of the seismic coefficient proposed in 1909 remained in seismic codes in different countries for many decades (see Sect. 2.6).
The most advanced of the engineers who studied the effects of the 1908 Messina earthquake was A. Danusso. He "was probably the first to propose a dynamic analysis method rather than static lateral force analysis method and, possibly for the first time in earthquake engineering, he stated that seismic demand does not depend upon the ground motion characteristics alone" (Sorrentino 2007). Danusso not only stated this relationship verbally, but presented his thinking mathematically. Danusso's approach was considered too much ahead of its time for practical implementation by the committee formed after the Messina earthquake, which found the static approach more practical for widespread application (Reitherman 2012, p. 193). As a matter of historical fact, dynamic analysis has not been implemented in seismic provisions for the next half of the century.
The committee's proposal to conventionally substitute dynamic actions with purely static ones in representing seismic effects had a great impact on the subsequent development of early earthquake engineering in Italy, since it simplified the design procedures but ruled out from the code any dynamic considerations until the mid-seventies (1974), when a design spectrum was introduced (Sorrentino 2007) and an up-to-date seismic code was adopted.
The Italians were the first to propose, in 1909, the equivalent static procedure for seismic analysis, and to implement it in a code. The procedure has been a constituent part of practically all seismic codes up until present times. Also, apparently the first dynamic seismic computations stem from Italy. However, their achievements did not have a widespread effect worldwide. It was the Japanese achievements, as described in the next section, which became more popular.
Japan
In Japan, in 1916 R. Sano proposed the use of seismic coefficients in earthquake resistant building design. "He assumed a building to be rigid and directly connected to the ground surface, and suggested a seismic coefficient equal to the maximum ground acceleration normalized to gravity acceleration. Although he noted that the lateral acceleration response might be amplified from the ground acceleration with lateral deformation of the structure, he ignored the effect in determining the seismic coefficient. He estimated the maximum ground acceleration in the Honjo and Fukagawa areas on alluvial soil in Tokyo to be 0.30 g and above on the basis of the damage to houses in the 1855 Ansei-Edo (Tokyo) earthquake, and that in the Yamanote area on diluvial hard soil to be 0.15 g" (Otani 2004). T. Naito, one of Sano's students at the University of Tokyo, became, like Sano, not just a prominent earthquake engineer but also one of the nation's most prominent structural engineers. He followed Sano's seismic coefficient design approach, usually using a coefficient of 1/15 (7%) to design buildings before the 1923 Kanto Earthquake. The coefficient was uniformly applied to masses up the height of the building (Reitherman 2012, p. 168).
The first Japanese building code was adopted in 1919. The 1923 Great Kanto earthquake led to the addition of an article in this code (adopted in 1924) to require the seismic design of all buildings for a seismic coefficient of 0.1. "From the incomplete measurement of ground displacement at the University of Tokyo, the maximum ground acceleration was estimated to be 0.3 g. The allowable stress in design was one third to one half of the material strength in the design regulations. Therefore, the design seismic coefficient 0.1 was determined by dividing the estimated maximum ground acceleration of 0.3 g by the safety factor of 3 of allowable stress" (Otani 2004).
The Japanese code, which applied to certain urban districts, was a landmark in the development of seismic codes worldwide. In the Building Standard Law, adopted in 1950, applicable to all buildings throughout Japan, the seismic coefficient was increased from 0.1 to 0.2 for buildings with heights of 16 m and less, increasing by 0.01 for every 4 m above (Otani 2004). Allowable stresses under temporary loads were set at twice the allowable stresses under permanent loads. From this year on, the seismic coefficients in Japan remained larger than elsewhere in the rest of the world. Later significant changes included the abolishment of the height limit of 100 ft in 1963. In 1981 the Building Standard Law changed. Its main new features included a seismic coefficient which varied with period, and two-level design. The first phase design was similar to the design method used in earlier codes. It was intended as a strength check for frequent moderate events. The second phase design was new. It was intended as a check for strength and ductility for a maximum expected event (Whittaker et al. 1998). It is interesting to note that, in Japan, the seismic coefficient varied with the structural vibration period only after 1981.
United States
Surprisingly, the strong earthquake which hit San Francisco in 1906 did not trigger the development of seismic provisions in the United States. Wind force was intended to protect buildings against both wind and earthquake damage. Design recommendations were intended only for buildings taller than 100 feet (30.5 m), or taller than three times the building's least dimension, and consisted of applying a 30 psf (1.44 kPa) wind load to the building's elevation. Later, the recommended wind load was reduced to 20 psf, and then to 15 psf (Diebold et al. 2008). At that time, however, no building code provisions existed for the design of shorter structures to resist wind or earthquake loads.
The first regulations on earthquake-resistant structures appeared in the United States only in 1927, after the earthquake in Santa Barbara in 1925. The provisions were contained in an appendix to the Uniform Building Code, and were not mandatory. The equivalent static procedure was used. The seismic coefficient was varied between 7.5 and 10% of the total dead load plus the live load of the building, depending on soil conditions. This was the first time that a building code had recognized the likelihood of the amplification of ground motion by soft soil (Otani 2004). After the 1925 Santa Barbara earthquake, some California municipalities did adopt mandatory seismic provisions in their building codes.
The first mandatory seismic codes used in the United States were published in 1933, after the 1933 Long Beach earthquake, which caused extensive damage to school buildings. Two California State Laws were enacted. The Field Act required the earthquake-resistant design and construction of all new public schools in California. The adopted regulations required that masonry buildings without frames be designed to resist a lateral force equal to 10% of the sum of the dead load and a fraction of the design live load. For other buildings the seismic coefficient was set at 2–5%. Shortly after this, the Riley Act was adopted with a mandatory seismic design coefficient of 2% of the sum of the dead load and live load for most buildings. At about the same time, in Los Angeles a lateral force requirement of 8% of the total weight and half of the design live load was imposed. This requirement was also adopted by the 1935 Uniform Building Code for the zone of highest seismicity (Berg 1983, pp. 25–26), whereas, recognizing the different levels of seismic risk in different regions, the seismic coefficients in the other two zones were lower.
Although the first regulations were based on the static concept, and did not take into account the fact that the structural acceleration (and thus the seismic load) depends on the vibration period of the building, the developers of the early codes were aware of the dynamic nature of the structural response and of the importance of the periods of vibration of buildings. Freeman wrote: "Those who have given the matter careful study recognize that as a means of lessening the amplitude of oscillation due to synchronism [i.e. resonance], it is extremely important to make the oscillation period of the building as small as practicable, or smaller than the oscillation period of the ground ordinarily found in great earthquakes." (Freeman 1932, p. 799). However, since the details of the ground motion, including the frequency content, were not known, any realistic quantitative considerations were impossible. The first generation of analysis methods evolved before being able to take into account response spectrum analysis and data from strong motion instruments, although the basic concept was known. Some of the most educated guesses of the frequency content of ground shaking were completely wrong considering today's knowledge. For example, Freeman (1930, p. 37) stated that "In Japan it has been noted that the destructive oscillations of the ground in an earthquake are chiefly those having a period from 1 to 1.5 s; therefore, some of the foremost Japanese engineers take great care in their designs to reduce the oscillation period of a building as nearly as practicable to from 0.5 to 0.6 s, or to less than the period of the most destructive quake, and also strive to increase the rigidity of the building as a whole in every practical way." Today, we know that, generally, in the 0.5 to 0.6 s range the spectral acceleration is usually larger than in the range from 1 to 1.5 s.
The first code, which related the seismic coefficient to the flexibility of the building, was enacted by the City of Los Angeles, in 1943. The level of the seismic coefficient was decreasing with the number of stories, reflecting the decrease of structural acceleration by increasing the flexibility and the natural period of the building. So, the building period was considered indirectly. This code also took into account the fact that the lateral force varies over the height of the structure. The building period became an explicit factor in the determination of seismic design forces only in 1956, when the City of San Francisco enacted a building code based on the recommendations produced by a joint committee of the Structural Engineers Association of Northern California and the San Francisco Section of the American Society of Civil Engineers (Berg 1983, pp. 26–27), published in 1951. The recommendations included an inverted triangle distribution of design lateral loads along the height of the building, which is still a basic feature of equivalent static lateral force procedures.
A theoretical basis for the consideration of the dependence of seismic load on the natural period of the building was made possible by the development of response spectra. Although the initial idea of the presentation of earthquake ground motion with spectra had appeared already in the early 1930s, the practical use of spectra has not been possible for over 30 years due to the lack of data about the ground motion during earthquakes, and because of the very extensive computational work required for the determination of spectra, which was virtually impossible without computers. For details on the historical development of response spectra, see, e.g. Chopra (2007) and Trifunac (2008).
The first code which took into account the impact of the energy dissipation capacity of structures in the inelastic range (although this was not explicitly stated in the code) was the SEAOC model code (the first "Blue Book"), in 1959. In order to distinguish between the inherent ductility and energy dissipation capacities of different structures, a coefficient K was introduced in the base shear equation. Its values were specified for four types of building construction. The basic seismic coefficient of 0.10 increased the most (by a factor of 1.33) in the case of wall structures, and decreased the most (by a factor of 0.67) in the case of space frames. According to Blume et al. (1961): "The introduction of K was a major step forward in code writing to provide in some degree for the real substance of the problem—energy absorption—and for the first time to recognize that equivalent acceleration or base shear coefficient C alone is not necessarily a direct index of earthquake resistance and public safety."
Seismic regulations at that time were mainly limited to analysis, and did not contain provisions on dimensioning and detailing. It was not until the end of the 1960s that, in the United States, provisions related to the detailing of ductile reinforced concrete frames were adopted.
An early appearance of Performance-Based Seismic Design can be found in the 1967 edition of the SEAOC Blue Book, where the following criteria were defined:
- 1.
Resist minor earthquakes without damage.
- 2.
Resist moderate earthquakes without structural damage, but with some nonstructural damage.
- 3.
Resist major earthquakes, of the intensity of severity of the strongest experienced in California, without collapse, but with some structural as well as nonstructural damage.
The first document, which incorporated most of the modern principles of seismic analysis, was ATC 3-06 (ATC 1978), which was released in 1978 (Fig. 2) as a result of years of work performed by many experts in the United States. As indicated by the title of the document, the document represented tentative provisions for the development of seismic regulations for buildings. Its primary purpose was to present the current state of knowledge in the fields of engineering seismology and earthquake engineering, in the form of a code. It contained a series of new concepts that significantly departed from existing regulations, so the authors explicitly discouraged the document's use as a code, until its usefulness, practicality, and impact on costs was checked. Time has shown that the new concepts have been generally accepted, and that the document was a basis for the subsequent guidelines and regulations in the United States and elsewhere in the world, with some exception in Japan.
In the document the philosophy of design in seismic regions, set forth in the 1967 SEAOC Blue Book, was followed, according to which the primary purpose of seismic regulations is the protection of human life, which is achieved by preventing the collapse of buildings or their parts, whereas in strong earthquakes damage and thus material losses are permitted. At the very beginning it was stated: "The design earthquake motions specified in these provisions are selected so that there is low probability of their being exceeded during the normal lifetime expectancy of the building. Buildings and their components and elements … may suffer damage, but should have a low probability of collapse due to seismic-induced ground shaking."
The document contained several significant differences compared to earlier seismic provisions. Seismic hazard maps, which represent the basis for design seismic loads, were based on a 90% probability that the seismic hazard, represented by the effective peak ground acceleration and the effective peak ground velocity (which serve as factors for constructing smoothed elastic response spectra), would not be exceeded in 50 years. This probability corresponds to a return period of the earthquake of 475 years. Buildings were classified into seismic hazard exposure groups. Seismic performance categories for buildings with design and analysis requirements depended on the seismicity index and the building seismic hazard exposure group. The analysis and design procedures were based upon a limit state that was characterized by significant yield rather than upon allowable stresses as in earlier codes. This was an important change which influenced also the level of the seismic coefficient.
An empirical force reduction factor R, called the "Response modification factor", was also introduced in ATC 3-06. Experience has shown that the great majority of well designed and constructed buildings survive strong ground motions, even if they were in fact designed for only a fraction of the forces that would develop if the structure behaved entirely as linearly elastic. A reduction of seismic forces is possible thanks to the beneficial effects of energy dissipation in ductile structures and inherent overstrength. Although the influence of the structural system and its capacity for energy dissipation has been recognized already in late 1950s, the force reduction factor (or simply R factor) in the current format was first proposed in ATC-3-06. Since then, R factor has been present, in various forms, in all seismic regulations (in the European standard EC8 it is called the behaviour factor q).
R factor allows, in a standard linear analysis, an approximate consideration of the favourable effects of the nonlinear behaviour of the structure, and therefore presents a very simple and practical tool for seismic design. However, it is necessary to bear in mind that describing a complex phenomenon of inelastic behaviour for a particular structure, by means of a single average number, can be confusing and misleading. For this reason, the R factor approach, although is very convenient for practical applications and has served the professional community well over decades, is able to provide only very rough answers to the problems encountered in seismic analysis and design. Also, it should be noted that "the values of R must be chosen and used with judgement", as stated in the Commentary to the ATC 03-6 document in Sect. 3.1. According to ATC-19 (ATC 1995), "The R factors for the various framing systems included in the ATC-3-06 report were selected through committee consensus on the basis of (a) the general observed performance of like buildings during past earthquakes, (b) estimates of general system toughness, and (c) estimates of the amount of damping present during inelastic response. Thus, there is little technical basis for the values of R proposed in ATC-3-06." Nevertheless, the order of magnitude of R factors (1.5 to 8, related to design at the strength level) has been widely used in many codes and has remained more or less unchanged until nowadays.
The model code recognized the existence of several "standard procedures for the analysis of forces and deformations in buildings subjected to earthquake ground motion", including Inelastic Response History Analysis. However, only two analysis procedures were specified in the document: Equivalent Lateral Force Procedure and Modal Analysis Procedure with one degree of freedom per floor in the direction being considered. In relation to modal analysis, it was stated in the Commentary in Sect. 3.5: "In various forms, modal analysis has been widely used in the earthquake-resistant design of special structures such as very tall buildings, offshore drilling platforms, dams, and nuclear power plants, but this is the first time that modal analysis has been included in the design provisions for buildings". The last part of this statement was true for the United States, but not worldwide, since modal analysis was adopted already in 1957 in the USSR's seismic code, as explained in the next section. In the Commentary it was recognized that the simple model used for modal analysis was "likely to be inadequate if the lateral motions in two orthogonal directions and the torsional motion are strongly coupled". In such a case and in some other cases, where the simple model was not adequate, the possibility of a "suitable generalization of the concepts" was mentioned.
Despite the tremendous progress which has been made in the field of earthquake engineering in recent decades, it can be concluded that the existing regulations, which of course contain many new features and improvements, are essentially still based on the basic principles that were defined in the ATC 3-06 document, with the partial exception of the United States, where the updating of seismic provisions has been the fastest.

The cover-page of ATC 3-06
Full size image
Other countries
At the beginning of 1930s, seismic codes were instituted only in Italy and Japan, and in a few towns in California. As mentioned in the previous section, the first mandatory seismic codes used in the United States were adopted in 1933. By the end of that decade, seismic codes were enacted in three more countries, New Zealand in 1935 (draft code in 1931), India in 1935, and Chile in 1939 (provisional regulations in 1930). In all cases a damaging earthquake triggered the adoption of seismic regulations (Reitherman 2012, p. 200 and p. 216). Seismic codes followed later in Canada in 1941 (Appendix to the National Building Code), Romania in 1942, Mexico in 1942, and Turkey in 1944 (a post-event response code had been adopted already in 1940.) The USSR's first seismic code was adopted in 1941 (Reitherman 2012, p. 288). The Standards and Regulations for Building in Seismic Regions, which was adopted in the USSR in 1957, included, apparently as the first code, the modal response spectrum method as the main analysis procedure (Korčinski 1964). This analysis procedure was later included in several European seismic codes and has remained the most popular procedure for seismic analysis in Europe, up until the present day. In EC8, too, it is the basic analysis method. In 1963 and 1964, respectively, Slovenia and the whole of the former Yugoslavia adopted seismic codes, which were with respect to the analysis method similar to the Soviet code. In China, the first code was drafted in 1955, but was not adopted (Reitherman 2012, p. 288). The first official seismic design code (The Code for the Seismic Design of Civil and Industrial Buildings) was issued in 1974.
Level of the design lateral seismic load
Interestingly, the level of the design horizontal seismic load (about 10% of the weight of the building), which was proposed in 1909 in Italy, and also used in Japan in the first half of the twentieth century, has been maintained in the seismic regulations for the majority of buildings up to the latest generation of regulations, when, on average, the design horizontal seismic load increased. An exception was Japan, where the seismic design loads increased to 20% of the weight already in 1950. The value of about 10%, proposed in Italy, was based on studies of three buildings which survived the 1908 Messina Earthquake. However, this study was, apparently, not known in other parts of the world. The Japanese engineer Naito wrote: "In Japan, as in other seismic countries, it is required by the building code [from 1924 onward] to take into account a horizontal force of at least 0.1 of the gravity weight, acting on every part of the building. But this seismic coefficient of 0.1 of gravity has no scientific basis either from past experience or from possible occurrence in the future. There is no sound basis for this factor, except that the acceleration of the Kwanto earthquake for the first strong portion as established from the seismographic records obtained at the Tokyo Imperial University was of this order." (Reitherman 2012, p. 172). Freeman (1930) expressed a similar opinion: "There is a current notion fostered by seismologists, and incorporated in the tentative building laws of several California cities, that the engineer should work to a seismic coefficient of 1/10 g. … Traced back to the source this rule is found to be a matter of opinion, not of measurement; a product, not of the seismometer, but of the "guessometer"."
Explanations as to why 10% of the weight of a building is an adequate design horizontal seismic load have changed over time. The seismic coefficient, which represents the ratio between the seismic load and the weight (plus some portion of the live load) depends on the ground acceleration and the dynamic characteristics of the structure. Initially, structures were assumed to be rigid, having the same acceleration as the ground. At the beginning of the twentieth century instruments for the recording of strong ground motion were not available. Some estimates of the level of maximum ground accelerations were obtained from observations of the sliding and overturning of rigid bodies such as stone cemetery monuments. Freeman (1932, p. 76) prepared a table with the relations between the Rossi–Forel intensity and peak ground acceleration, as proposed by six different authors. The values of accelerations in m/s2 for intensities VIII, IX and X were within the ranges 0.5–1.0 (mean 0.58), 1.0–2.0 (mean 1.23) and 2.5–3.0 (mean 2.62), respectively. Note that the intensity IX on the Rossi-Forel scale ("Partial or total destruction of some buildings") approximately corresponds to intensity IX according to the EMS. The data clearly indicate that the values of the peak ground acceleration were grossly underestimated.
The first strong motion accelerograms were recorded only in 1933, during the Long Beach earthquake. Maximum acceleration values did not significantly deviate from 0.1 g until 1940, when the famous El Centro 1940 accelerogram, with a maximum acceleration of more than 0.3 g, was recorded. At the time of the 1971 San Fernando Earthquake, the peak ground acceleration produced by that earthquake tripled what most engineers of the time thought possible (Reitherman 2012, p. 272). With the awareness that ground acceleration can be much higher than expected, and that very considerable dynamic amplification can occur if the period of the structure is in the range of the predominant periods of the ground motion, both resulting in accelerations of the structure much greater than 0.1 g, it was possible to justify a seismic coefficient of about 10% only due to the favourable influence of several factors, mainly energy dissipation in the inelastic range, and so-called overstrength, i.e. the strength capacity above that required by the code design loads. In the 1974 edition of the SEAOC code, for the first time the basis for the design load levels was made explicit in the Commentary: "The minimum design forces prescribed by the SEAOC Recommendations are not to be implied as the actual forces to be expected during an earthquake. The actual motions generated by an earthquake may be expected to be significantly greater than the motions used to generate the prescribed minimum design forces. The justification for permitting lower values for design are many-fold and include: increased strength beyond working stress levels, damping contributed by all the building elements, an increase in ductility by the ability of members to yield beyond elastic limits, and other redundant contributions. (SEAOC Seismology Committee 1974, p. 7-C)" (Reitherman 2012, p. 277). More recently, other influences have been studied, e.g. the shape of the uniform hazard spectrum used in seismic design.
In Japan, already Sano and Naito advocated making structures as stiff as possible. Designing stiff and strong structures has remained popular in Japan until the present time. Otani (2004) wrote: "The importance of limiting story drift during an earthquake by providing large stiffness and high lateral resistance should be emphasized in earthquake engineering." Consequently, in Japan the design seismic lateral loads have been, since 1950, generally larger than in the rest of the world. More recently, the level of the design seismic loads has gradually increased, on average, also in other countries. The reasons for this trend are increasing seismic hazard, estimated by new probabilistic seismic hazard analyses and new ground motion databases, and also better care for the limitation of damage.
When comparing seismic coefficients, it should be noted that the design based on allowable stresses used in early codes has been changed to limit stress design, so that the values of seismic coefficients may not be directly comparable.
Present: gradual implementation of nonlinear methods
Introduction
Most buildings experience significant inelastic deformations when affected by strong earthquakes. The gap between measured ground accelerations and the seismic design forces defined in codes was one of the factors which contributed to thinking in quantitative terms beyond the elastic response of structures. At the Second World Conference on Earthquake Engineering in 1960 several leading researchers presented some early significant papers about inelastic response. However, there was a long way to go before the explicit nonlinear analysis found its way into more advanced seismic codes. Initially the most popular approach was the use of force reduction factors, and this approach is still popular today. Although this concept for taking into account the influence of inelastic behaviour in linear analysis has served the profession well for several decades, a truly realistic assessment of structural behaviour in the inelastic range can be made only by means of nonlinear analysis. It should be noted, however, that "good nonlinear analysis will not trigger good designs but it will, hopefully, prevent bad designs." (Krawinkler 2006). Moreover: "In concept, the simplest method that achieves the intended objective is the best one. The more complex the nonlinear analysis method, the more ambiguous the decision and interpretation process is. … Good and complex are not synonymous, and in many cases they are conflicting." (Krawinkler 2006).
The current developments of the analysis procedures in seismic codes are characterized by a gradual implementation of nonlinear analysis, which should be able to explicitly simulate the second basic feature of structural response to strong seismic ground motion, i.e. inelastic behaviour. For such nonlinear analyses, data about the structure have to be known, so they are very well suited for the analysis of existing structures. In the case of newly designed structures, a preliminary design has to be made before starting a nonlinear analysis. Typical structural response measures that form the output from such an analysis (also called "engineering demand parameters") are: the storey drifts, the deformations of the "deformation-controlled" components, and the force demands in "force-controlled" (i.e. brittle) components that, in contemporary buildings, are expected to remain elastic. Basically, a designer performing a nonlinear analysis should think in terms of deformations rather than in terms of forces. In principle, all displacement-based procedures require a nonlinear analysis.
There are two groups of methods for nonlinear seismic analysis: response-history analysis, and static (pushover-based) analysis, each with several options. They will be discussed in the next two sections. An excellent guide on nonlinear methods for practicing engineers was prepared by Deierlein et al. (2010).
Nonlinear response history analysis (NRHA)
Nonlinear response history analysis (NRHA) is the most advanced deterministic analysis method available today. It represents a rigorous approach, and is irreplaceable for the research and for the design or assessment of important buildings. However, due to its complexity, it has, in practice, been mostly used only for special structures. NRHA is not only computationally demanding (a problem whose importance has been gradually reduced due to the development of advanced hardware and software), but also requires additional data which are not needed in pushover-based nonlinear analysis: a suite of accelerograms, and data about the hysteretic behaviour of structural members. A consensus about the proper way to model viscous damping, in the case of inelastic structural response, has not yet been reached. A wide range of assumptions are needed in all steps of the process, from ground motion selection to nonlinear modelling. Many of these assumptions are based on judgement. Blind predictions of the results of a bridge column test (see Sect. 1) are a good example of potential problems which can arise when NRHA is applied. Moreover, the complete analysis procedure is less transparent than in the case of simpler methods. For this reason, the great majority of codes which permit the use of NRHA require an independent review of the results of such analyses.
The advantages and disadvantages of NRHA have been summarized in a recent paper by the authors representing both academia and practice in the United States (Haselton et al. 2017). The advantages include "the ability to model a wide variety of nonlinear material behaviors, geometric nonlinearities (including large displacement effects), gap opening and contact behavior, and non-classical damping, and to identify the likely spatial and temporal distributions of inelasticity. Nonlinear response history analysis also has several disadvantages, including increased effort to develop the analytical model, increased time to perform the analysis (which is often complicated by difficulties in obtaining converged solutions), sensitivity of computed response to system parameters, large amounts of analysis results to evaluate and the inapplicability of superposition to combine non-seismic and seismic load effects." Moreover, "seemingly minor differences in the way damping is included, hysteretic characteristics are modeled, or ground motions are scaled, can result in substantially different predictions of response. … The provisions governing nonlinear response history analysis are generally non-prescriptive in nature and require significant judgment on the part of the engineer performing the work."
To the author's knowledge, the first code in which the response-history analysis was implemented was the seismic code adopted in the former Yugoslavia in 1981 (JUS 1981). In this code, a "dynamic analysis method", meant as a linear and nonlinear response-history analysis, was included. In the code, it was stated: "By means of such an analysis the stresses and deformations occurring in the structure for the design and maximum expected earthquake can be determined, as well as the acceptable level of damage which may occur to the structural and non-structural elements of the building in the case of the maximum expected earthquake." The application of this method was mandatory for all out-of-category, i.e. very important buildings, and for prototypes of prefabricated buildings or structures which are produced industrially in large series. Such a requirement was very advanced (and maybe premature) at that time (Fischinger et al. 2015).
In the USA, the 1991 Uniform Building Code (UBC) was the first to include procedures for the use of NRHA in design work. In that code, response-history analysis was required for base-isolated buildings and buildings incorporating passive energy dissipation systems (Haselton et al. 2017). After that, several codes in different countries included NRHA, typically with few accompanying provisions, leaving the analyst with considerable freedom of choice. Reasonably comprehensive provisions/guidelines have been prepared only for the most recent version of ASCE 7 standard, i.e. ASCE 7-16 (ASCE 2017). An overview of the status of nonlinear analysis in selected countries is provided in Sect. 3.5. In this paper, NRHA will not be discussed in detail.
Nonlinear static (pushover) analysis
A pushover-based analysis was first introduced in the 1970s as a rapid evaluation procedure (Freeman et al. 1975). In 1980s, it got the name Capacity Spectrum Method (CSM). The method was also developed into a design verification procedure for the Tri-services (Army, Navy, and Air Force) "Seismic Design Guidelines for Essential Buildings" manual (Army 1986). An important milestone was the paper by Mahaney et al. (1993) in which the acceleration–displacement response spectrum (ADRS, later also called AD) format was introduced, enabling visualization of the assessment procedure. In 1996, CSM was adopted in the guidelines for Seismic Evaluation and Retrofit of Concrete Buildings, ATC 40 (ATC 1996). In order to account for the nonlinear inelastic behaviour of a structural system, effective viscous damping values are applied to the linear-elastic response spectrum (i.e. an "overdamped spectrum") in all CSM formulations. In the N2 method, initially developed by Fajfar and Fischinger (1987, 1989), and later formulated in acceleration–displacement (AD) format (Fajfar 1999, 2000), inelastic spectra are used instead of overdamped elastic spectra. The N2 method has been adopted in EC8 in 2004. In FEMA 273 (1997), the target displacement was determined by the "Coefficient Method". This approach, which has remained in all following FEMA documents, and has also been adopted in the ASCE 41-13 standard (ASCE 2014), resembles the use of inelastic spectra. In the United States and elsewhere, the use of pushover-based procedures has accelerated since the publication of the ATC 40 and FEMA 273 documents. In this section, the discussion will be limited to the variant of the pushover-based method using inelastic spectra. A comprehensive summary of pushover analysis procedures is provided in Aydinoğlu and Önem (2010).
A simple pushover approach, which could be applied at the storey level and used for the analysis of the seismic resistance of low-rise masonry buildings, was developed in the late 1970s by Tomaževič (1978). This approach was adopted also in a regional code for the retrofitting of masonry buildings after the 1976 Friuli earthquake in the Italian region of Friuli-Venezia Guilia (Regione Autonoma Friuli-Venezia Giulia 1977).
Pushover-based methods combine nonlinear static (i.e. pushover) analysis with the response spectrum approach. Seismic demand can be determined for an equivalent single-degree-of-freedom (SDOF) system from an inelastic response spectrum (or an overdamped elastic response spectrum). A transformation of the multi-degree-of-freedom (MDOF) system to an equivalent SDOF system is needed. This transformation, which represents the main limitation of the applicability of pushover-based methods, would be exact only in the case that the analysed structure vibrated in a single mode with a deformation shape that did not change over time. This condition is, however, fulfilled only in the case of a linear elastic structure with the negligible influence of higher modes. Nevertheless, the assumption of a single time-invariant mode is used in pushover-based methods for inelastic structures, as an approximation.
Pushover-based analyses can be used as a rational practice-oriented tool for the seismic analysis. Compared to traditional elastic analyses, this kind of analysis provides a wealth of additional important information about the expected structural response, as well as a helpful insight into the structural aspects which control performance during severe earthquakes. Pushover-based analyses provide data on the strength and ductility of structures which cannot be obtained by elastic analysis. Furthermore, they are able to expose design weaknesses that could remain hidden in an elastic analysis. This means that in most cases they are able to detect the most critical parts of a structure. However, special attention should be paid to potential brittle failures, which are usually not simulated in the structural models. The results of pushover analysis must be checked in order to find out if a brittle failure controls the capacity of the structure.
For practical applications and educational purposes, graphical displays of the procedure are extremely important, even when all the results can be obtained numerically. Pushover-based methods experienced a breakthrough when the acceleration–displacement (AD) format was implemented. Presented graphically in AD format, pushover-based analyses can help designers and researchers to better understand the basic relations between seismic demand and capacity, and between the main structural parameters determining the seismic performance, i.e. stiffness, strength, deformation and ductility. They are a very useful educational tool for the familiarizing of students and practising engineers with general nonlinear seismic behaviour, and with the seismic demand and capacity concepts.
Pushover-based methods are usually applied for the performance evaluation of a known structure, i.e. an existing structure or a newly designed one. However, other types of analysis can, in principle, also be applied and visualised in the AD format. Basically, four quantities define the seismic performance: strength, displacement, ductility and stiffness. Design and/or performance evaluation begins by fixing one or two of them; the others are then determined by calculations. Different approaches differ in the quantities that are chosen at the beginning of the design or evaluation. Let's assume that the approximate mass is known. In the case of seismic performance evaluation, stiffness (period) and strength of the structure have to be known; the displacement and ductility demands are calculated. In direct displacement-based design, the starting points are typically the target displacement and/or ductility demands. The quantities to be determined are stiffness and strength. The conventional force-based design typically starts from the stiffness (which defines the period) and the approximate global ductility capacity. The seismic forces (defining the strength) are then determined, and finally the displacement demand is calculated. Capacity in terms of spectral acceleration can be determined from the capacity in terms of displacements. All these approaches can be easily visualised with the help of Fig. 3.
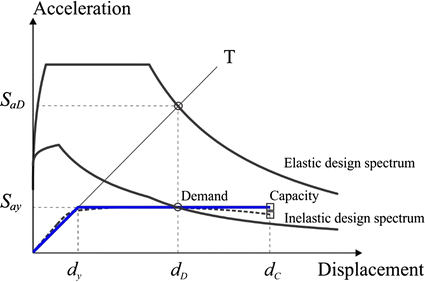
Comparison of demand and capacity in the acceleration–displacement (AD) format
Full size image
Note that, in all cases, the strength is the actual strength and not the design base shear according to seismic codes, which is in all practical cases less than the actual strength. Note also that stiffness and strength are usually related quantities.
Compared to NRHA, pushover-based methods are a much simpler and more transparent tool, requiring simpler input data. The amount of computation time is only a fraction of that required by NRHA and the use of the results obtained is straightforward. Of course, the above-listed advantages of pushover-based methods have to be weighed against their lower accuracy compared to NRHA, and against their limitations. It should be noted that pushover analyses are approximate in nature, and based on static loading. They have no strict theoretical background. In spite of extensions like those discussed in the next section, they may not provide acceptable results in the case of some building structures with important influences of higher modes, including torsion. For example, they may detect only the first local mechanism that will form, while not exposing other weaknesses that will be generated when the structure's dynamic characteristics change after formation of the first local mechanism. Pushover-based analysis is an excellent tool for understanding inelastic structural behaviour. When used for quantification purposes, the appropriate limitations should be observed. Additional discussion on the advantages, disadvantages and limitations of pushover analysis is available in, for instance Krawinkler and Seneviratna (1998), Fajfar (2000) and Krawinkler (2006).
The influence of higher modes in elevation and in plan (torsion)
The main assumption in basic pushover-based methods is that the structure vibrates predominantly in a single mode. This assumption is sometimes not fulfilled, especially in high-rise buildings, where higher mode effects may be important along the height of the building, and/or in plan-asymmetric buildings, where substantial torsional influences can occur. Several approaches have been proposed for taking the higher modes (including torsion) into account. The most popular is Modal pushover analysis, developed by Chopra and Goel (2002). Some of the proposed approaches require quite complex analyses. Baros and Anagnostopoulos (2008) wrote: "The nonlinear static pushover analyses were introduced as simple methods … Refining them to a degree that may not be justified by their underlying assumptions and making them more complicated to apply than even the nonlinear response-history analysis … is certainly not justified and defeats the purpose of using such procedures."
In this section, the extended N2 method (Kreslin and Fajfar 2012), which combines two earlier approaches, taking into account torsion (Fajfar et al. 2005) and higher mode effects in elevation (Kreslin and Fajfar 2011), into a single procedure enabling the analysis of plan-asymmetric medium- and high-rise buildings, will be discussed. The method is based on the assumption that the structure remains in the elastic range in higher modes. The seismic demand in terms of displacements and storey drifts can be obtained by combining together the deformation quantities obtained by the basic pushover analysis and those obtained by the elastic modal response spectrum analysis. Both analyses are standard procedures which have been implemented in most commercial computer programs. Thus the approach is conceptually simple, straightforward, and transparent.
In the elastic range, the vibration in different modes can be decoupled, with the analysis performed for each mode and for each component of the seismic ground motion separately. The results obtained for different modes using design spectra are then combined together by means of approximate combination rules, like the "Square Root Sum of Squares" (SRSS) or "Complete Quadratic Combination" (CQC) rule. The SRSS rule can be used to combine the results for different components of the ground motion. This approach has been widely accepted and used in practice, in spite of the approximations involved in the combination rules. In the inelastic range, the superposition theoretically does not apply. However, the coupling between vibrations in different modes is usually weak (Chopra 2017, p. 819). Thus, for the majority of structures, some kind of superposition can be applied as an approximation in the inelastic range, too.
It has been observed that higher mode effects depend to a considerable extent on the magnitude of the plastic deformations. In general, higher mode effects in plan and in elevation decrease with increasing ground motion intensity. Thus, conservative estimates of amplification due to higher mode effects can usually be obtained by elastic modal response spectrum analysis. The results of elastic analysis, properly normalised, usually represent an upper bound to the results obtained for different intensities of the ground motion in those parts of the structure where higher mode effects are important, i.e. in the upper part of medium- or high-rise buildings, and at the flexible sides of plan-asymmetric buildings. An exception are the stiff sides of plan-asymmetric buildings. If the building is torsionally stiff, usually a de-amplification occurs at the stiff side, which mostly decreases with increasing plastic deformations. If the building is torsionally flexible, amplifications may also occur at the stiff side, which may be larger in the case of inelastic behaviour than in the case of elastic response.
The extended N2 method has been developed taking into account most of the above observations. It is assumed that the higher mode effects in the inelastic range are the same as in the elastic range, and that a (in most cases conservative) estimate of the distribution of seismic demand throughout the structure can be obtained by enveloping the seismic demand in terms of the deformations obtained by the basic pushover analysis, which neglects higher mode effects, and the normalized (the same roof displacement as in pushover analysis) results of elastic modal analysis, which includes higher mode effects. De-amplification due to torsion is not taken into account. The target displacements are determined as in the basic N2 method, or by any other procedure. Higher mode effects in plan (torsion) and in elevation are taken into account simultaneously. The analysis has to be performed independently for two horizontal directions of the seismic action. Combination of the results for the two horizontal components of the seismic action is performed only for the results obtained by elastic analysis. The combined internal forces, e.g. the bending moments and shear forces, should be consistent with the deformations. For more details, see Kreslin and Fajfar (2012) and Fardis et al. (2015). Note that a variant of Modal pushover analysis is also based on the assumption that the vibration of the building in higher modes is linearly elastic (Chopra et al. 2004).
Two examples of the results obtained by the extended N2 method are presented in Figs. 4 and 5. Figure 4 shows the storey drifts along the elevation of the 9-story high steel "Los Angeles building" which was investigated within the scope of the SAC project in the United States. Shown are results of the NRHA analysis, of the basic pushover analysis, of the elastic modal response spectrum analysis, and of the extended N2 method. Figure 5 shows the normalized displacements, i.e. the displacements at different locations in the plan divided by the displacement of the mass centre CM, obtained by NRHA for different intensities of ground motion, by the basic pushover analysis, by the elastic modal response spectrum analysis, and by the extended N2 method. The structural model corresponds to the SPEAR building which was tested within the scope of an European project.
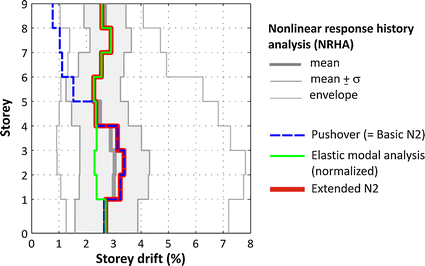
(adapted from Kreslin and Fajfar 2011)
Comparison of storey drifts obtained by different procedures for the 9-storey LA building
Full size image
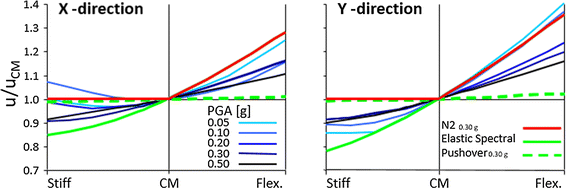
(adapted from Fajfar et al. 2005)
Comparison of normalized roof displacement in plan obtained by NRHA analysis (mean values) for different intensities, elastic response spectrum analysis, pushover analysis, and the extended N2 method for the SPEAR building
Full size image
The extended N2 method will be most probably implemented in the expected revised version of EC8. At the time when the current Part 1 of EC8 was finalised, the extended version of the N2 method for plan-asymmetric buildings had not yet been fully developed. Nevertheless, based on the preliminary results, the clause "Procedure for the estimation of torsional effects" was introduced, in which it was stated that "pushover analysis may significantly underestimate deformations at the stiff/strong side of a torsionally flexible structure". It was also stated that "for such structures, displacements at the stiff/strong side shall be increased, compared to those in the corresponding torsionally balanced structure" and that "this requirement is deemed to be satisfied if the amplification factor to be applied to the displacements of the stiff/strong side is based on the results of an elastic modal analysis of the spatial model".
ASCE 41-13 basically uses the same idea of enveloping the results of the two analysis procedures in order to take into account the higher modes in elevation. In C7.3.2.1 it is stated "Where the NSP [Nonlinear Static Procedure] is used on a structure that has significant higher mode response, the LDP [Linear Dynamic Procedure, typically the modal response spectrum analysis] is also used to verify the adequacy of the evaluation or retrofit." The same recommendation is included in the very recent New Zealand guidelines (NZSEE 2017).
Nonlinear analysis in current codes
In this section, an attempt has been made to present an overview of the status of nonlinear analysis in the codes of different countries and of its use in practice. The material is based on the responses of the author's colleagues to a quick survey and on the available literature. It can be observed that nonlinear analysis (NHRA more often than pushover analysis) has been adopted in the majority of the respective countries as an optional procedure which, however, is in some codes the mandatory for tall buildings and for special structural systems, e.g. base-isolated buildings. In next sections, these countries and regions are listed in alphabetical order.
Canada
The latest approved version of the National Building Code of Canada is NBCC 2015. The code applies only to new buildings; there is no code for existing building. The Code is accompanied by a Commentary, which explains the intent of the code and how best to meet it. The provisions or specifications given in the Commentary are not mandatory, but act as guidelines. According to the Code, dynamic analysis is the preferred method of analysis. The dynamic analysis procedure may be response spectrum analysis, or linear time history analysis, or NRHA. In the last case a special study is required. The Commentary gives the specifics of the nonlinear analysis procedure and the conditions for a special study. Inter alia, an independent design review is required when NRHA is used. Consultants (particularly in British Columbia) often use response spectrum analysis for the design of high-rise irregular buildings, and for important buildings such as hospitals. Linear time history analysis is used only infrequently, whereas NRHA is not used in practice. Nonlinear analysis is used mainly for the evaluation of existing buildings. It is considered to be a very complicated task, being hardly ever justified for the design of a new building. Pushover analysis is not directly referred to in the NBCC.
Chile
The present design building code, (NCh 433) does not consider and does not allow nonlinear analysis (static or dynamic). Nevertheless, all buildings taller than four storeys are required to have a peer review. This review is generally done using parallel modelling and design. Seismic designs of some of the tallest buildings have been reviewed using pushover analysis. The code for base isolated buildings (NCh2745) requires NRHA in all irregular or tall isolated structures. Nonlinear properties are considered, at least for isolators. The code for industrial structures (NCh2369) has always allowed for nonlinear analysis (static and dynamic) but it has been used only on rare occasions, for structures with energy dissipation devices and complex structures. The new design building code, which has been drafted and is currently undergoing an evaluation process, does, however, take into account nonlinear analysis and performance-based design. Nonlinear structural analysis is taught at the undergraduate level at the universities. So young designers are able to use standard software that includes nonlinear static and dynamic analysis. In advanced design offices, nonlinear analysis is regularly used.
China
According to the 2010 version of the Chinese Code for Seismic Design of Buildings (GB 50011-2010), linear analysis (static or dynamic) is the main procedure. "For irregular building structures with obvious weak positions that may result in serious seismic damage, the elasto-plastic deformation analysis under the action of rare earthquake shall be carried out … In this analysis, the elasto-plastic static analysing method or elasto-plastic time history analysing method may be adopted depending on the structural characteristics". In some cases simplified nonlinear analysis can be also used. The code has a separate section for performance-based design, where it is stated that either linear analysis with increased damping, or nonlinear static or dynamic analysis can be used for performance states where nonlinear behaviour is expected. In the case of tall buildings, linear analysis is performed for the frequent earthquake level, whereas nonlinear analysis, including pushover analysis and NHRA, is used for the major earthquake level. The type of the required nonlinear analysis depends on the height and complexity of the structure. NRHA should be performed for buildings with heights of more than 200 m or with severe irregularities. Buildings higher than 300 m have to be analyzed using two or more different computer programs in order to validate the results (Jiang et al. 2012).
Europe
Most countries in Europe use the European standard EN 1998 Design of structures for earthquake resistance (called Eurocode 8 or EC8), which consists of six parts. Part 1, enforced in 2004, applies to new buildings, and Part 3, enforced in 2005, applies to existing buildings. The main analysis procedure is linear modal response spectrum analysis. The equivalent static lateral force procedure can be used under some restrictions. Nonlinear analysis is permitted. It can be static (pushover) or NRHA. The basic requirements for pushover analysis (the N2 method) are provided in the main text of Part 1, whereas more details are given in an informative annex. NRHA is regulated very deficiently by only three clauses. In the revised version, which is currently under development, pushover analysis will play a more prominent role, whereas, in the draft of the revision, NRHA is still not adequately regulated. In practice, the use of NRHA is extremely rare, whereas the use of pushover analysis varies from country to country.
India
Nonlinear analysis has not been included in the building code, and is not used in design. No changes are expected in the near future.
Iran
The Iranian Seismic Code was updated in 2014 to the 4th Edition. The analysis procedures include linear procedures, i.e. linear static, response spectrum, and linear response history analyses, and nonlinear procedures, i.e. pushover and NRHA. The linear static procedure is permitted for all buildings with heights of up to 50 m with the exception of some irregular cases, whereas response spectrum and linear response history analyses are permitted for all cases. Pushover analysis and NRHA can be used for all kinds of buildings. However, one of the linear procedures should also be performed in addition to nonlinear analysis. In the 50% draft version of the code, the use of nonlinear analyses was encouraged by a 20% reduction in force and drift limitations. In the final version, such a reduction is not permitted. The pushover method is based on the EC8 and NEHRP 2009 approaches. A standard for the seismic rehabilitation of existing buildings (Standard No. 360) exists. The first edition was mainly based on FEMA 356, and the second edition is based mainly on ASCE 41-06. This standard has been widely used in retrofitting projects, and also sometimes in design projects. Pushover analysis is the most frequently used analysis method in seismic vulnerability studies of existing public and governmental buildings. It is used for all building types, including masonry buildings. The most popular is the coefficient method.
Japan
The seismic design requirements are specified in the Building Standard Law. In 1981 a two-phase seismic design procedure was introduced, which is still normally used in design offices. The performance-based approach was implemented in 2000. Most engineered steel and concrete buildings are designed with the aid of nonlinear analysis (pushover or NRHA) in the second phase design. For buildings with heights of less than 60 m, pushover analysis is usually conducted in order to check the ultimate resistance of members and of the building. For high-rise buildings (with heights of more than 60 m), NRHA is required. Usually, first a pushover analysis of a realistic 3D model is conducted in order to define the relationship between the storey-shear and the storey-drift for each storey. These relationships are modelled by means of trilinear models. NRHA is performed for a simplified structural model where stick element models (shear or shear-flexure model) are used. Very rarely, a complex 3D model is directly used for NRHA. Designs are subject to technical peer review. The software needs to be evaluated by the Minister of the Land, Infrastructure, Transport and Tourism.
Mexico
The present code (MOC-2008) permits NRHA. The design base shear determined in dynamic analysis should not be less than 80% of the base shear determined by the static force procedure. Over the last 10 years NRHA has been used in Mexico City for very tall buildings (having from 30 to 60 storeys), mainly because this was required by international insurance companies. Static pushover analysis has been seldom used in practice. The new code, which is expected to be published at the end of 2017, will require dynamic spectral analysis for the design of the majority of structures, and the results will need to be verified by a NRHA in the case of very tall or large buildings non-complying with regularity requirements.
New Zealand
The NZ seismic standard (NZS1170.5) requires either a response spectrum analysis or a response-history analysis (linear or nonlinear) in order to obtain local member actions in tall or torsionally sensitive buildings. Even in the case of other buildings (which are permitted to be analysed by equivalent static linear analysis), the designers can opt to use more advanced analysis methods (so using pushover analysis in such cases may perhaps be argued to be acceptable). In practice, majority of structures are still designed using the linear static approach, but NRHA is becoming more and more common. The use of the linear static method is also the most common method used when assessing existing buildings, although pushover analysis has also been used. Very recently, technical guidelines for the engineering assessment of existing buildings were published (NZSEE 2017). They recommend the use of SLaMA (Simple Lateral Mechanism Analysis) as a starting point for any detailed seismic assessment. SLaMA represents a form of static nonlinear (pushover) analysis method, which is a hand calculation upper-bound approach defined as "an analysis involving the combination of simple strength to deformation representations of identified mechanisms to determine the strength to deformation (push-over) relationship for the building as a whole". In addition to standard linear analyses and SLaMA, the standard nonlinear pushover procedure and NRHA are also included in the guidelines.
Taivan
The seismic analysis procedures have remained practically unchanged since the 2005 version of the provisions. In the case of new buildings, linear analysis using the response spectrum method is a very common practice, regardless of the building's regularity or height. Pushover analysis is also very popular as a means to determine the peak roof displacement, the load factor to design the basement, the ground floor diaphragm, and the foundation or piling. Linear response history analysis is not common. NRHA is sometimes conducted for buildings using oil or metallic dampers. In the case of tall buildings with or without dampers, some engineers use general-purpose computer programs to evaluate the peak story drift demands, the deformation demands on structural members, and the force demands on columns, the 1st floor diaphragm, and the foundation or basement. Base-isolated buildings have become more popular, and engineers like to use nonlinear springs for base isolators only. Existing government buildings have to be retrofitted up to the current standard for new constructions. Pushover analysis is very common for the evaluation of existing condition of buildings and verifying the retrofit design.
Turkey
In the Specification for buildings to be built in seismic zones (which was adopted in 2007) nonlinear analysis is mentioned but not emphasized. A special chapter was added to the Code in 2007, which is devoted to the seismic assessment and retrofitting of existing buildings; it specifies the use of both the single-mode and the multi-mode pushover procedures as well as the use of NRHA. However, these methods have not been widely used in practice for assessment and retrofitting purposes. The new code (the Turkish Seismic Code for Building Structures) will be published by the end of 2017 and will be enforced after a 1-year transition period. In addition to the traditional force-based design, which is based entirely on linear elastic analysis, the code contains a new section on displacement (performance) based design, where the entire analysis is nonlinear, either pushover (several different types of pushover analysis can be used) or response-history. Tall buildings, the isolation level of the base isolated buildings and all other buildings in seismic zones 1 and 2 (the most severe categories, out of 4), existing or new, which require advanced seismic performance, have to be modelled by considering the nonlinear response. For existing buildings, in addition to nonlinear procedures, a new displacement-based equivalent linear procedure can also be used for buildings where a soft storey mechanism is not expected. NRHA has been occasionally used for tall buildings (since 2007) based on a draft code prepared for the seismic design of tall buildings upon the request of the Istanbul Metropolitan Municipality. Except in the case of tall and base isolated buildings, there have so far been almost no practical applications of nonlinear analysis. For seismic rehabilitation, single mode pushover analysis has been used in the past.
United States
The structure of the guidelines, standards, and codes is complicated. The most representative seem to be the ASCE standards. According to ASCE 7-16, which applies to new structures, NRHA is permitted, but is not required. It is regulated in Chapter 16, which has been completely rewritten in the last version of the standard. A linear analysis has to be performed in addition to NRHA. An independent structural design review is required. Existing structures are regulated by ASCE 41-13. Nonlinear procedures are permitted for all buildings. They are used for the analysis of buildings where linear procedures are not permitted. There are some limitations on the use of nonlinear static (pushover) analysis, whereas NRHA can be used for all structures. However, when NRHA is used, "the authority having jurisdiction shall consider the requirement of review and approval by an independent third-party engineer with experience in seismic design and nonlinear procedures". Special Seismic Design Guidelines for Tall Buildings exist (PEER 2017) which present a recommended alternative to the prescriptive procedures for the seismic design of buildings contained in standards such as ASCE 7. NRHA is required for MCER (Maximum Considered Earthquake) evaluation. It should be performed in accordance with the provisions of ASCE 7-16, Chapter 16. Nonlinear static analysis may be used to supplement nonlinear dynamic analysis as an aid to understanding the yield hierarchy, overstrength, and effective values of R factors when this is deemed desirable. In general, nonlinear analysis has been well established in the United States.
Future: risk assessment. Is it a feasible option for codes?
Introduction
Historically, among the three features of seismic analysis, dynamics has been implemented first, followed by inelasticity. The remaining feature is probability, which has not yet found its way into the practice, with the exception of some very important structures, although the theoretical background and computational procedures have been already developed. The evolution of reliability concepts and theory in structural design are described in fib (2012).
The seismic response of structures is characterized by large uncertainties, especially with respect to the ground motion, but also in the structural modelling, so that, in principle, a probabilistic approach would be appropriate for seismic performance assessment. However, an average engineer is not familiar with probabilistic methods and is very hesitant to use them. Also, a large part of the research community is skeptical about explicit probabilistic approaches other than those used in seismic hazard analysis.
The results of a quick survey which was performed among some colleagues from different countries indicate that almost all of them doubt that an explicit probabilistic approach will be adopted in future building codes in their countries, at least in the near future, with the exception of the United States, where this has already occurred to some extent in ASCE 7, but has been very rarely used in practice. A more realistic possibility is the adoption of an explicit quantitative consideration of risk in codes for critical infrastructure.
Nevertheless, in the long term, it will be difficult to completely avoid quantitative determination of risk. Also due to the public pressure on loss minimisation in addition to life safety in most developed countries with high seismicity, the profession will be sooner or later forced to accept some kind of risk-based design and assessment, at least for a better calibration of different safety factors and force reduction factors used in codes. Information on seismic risk would also facilitate discussions of design options between designers, building owners and other stakeholders. However, the mandatory use of explicit probabilistic approaches in seismic building codes, if it will ever happen, is still very distant. "This time lag, however, should be regarded as an opportunity to familiarize with the approaches before actual application." (fib 2012, Preface). The prerequisite for possible implementation of quantitative risk assessment in the codes are reasonably reliable input data and highly simplified procedures, which are presented in a format that is familiar to engineers, and which require only a small amount of additional effort and competence. Inclusion of optional reliability-based material in the seismic codes would help due to its educational role. The very first step has been very recently already taken in Europe with a draft informative annex to EC8, as described in the next section.
Current state of probabilistic analysis in seismic codes
Probabilistic seismic hazard analysis (PSHA) is already well established. It is, as a rule, performed by specialists and not by average designers. Since the early 1970s, it has been used for the preparation of seismic hazard maps and for the determination of the seismic design parameters of important structures. In the majority of codes, including EC8, the design ground motion corresponds to a return period of 475 years, which corresponds to a 10% probability of exceedance in 50 years. Some codes use the return period of 2500 years (a 2% probability of exceedance in 50 years). The analysis of structures is typically performed by deterministic analysis, using the ground motion parameters corresponding to a prescribed return period of the ground motion. In this analysis, the uncertainties are implicitly taken into account by means of various safety factors. An explicit probabilistic approach, which allows for the explicit quantification of the probability of exceedance of different limit states, has not yet been implemented in building seismic codes (with the exception of the ASCE-7 standard, as explained later in this section). When using current seismic codes, "at the end of the design process there is no way of evaluating the reliability actually achieved. One can only safely state that the adoption of all the prescribed design and detailing rules should lead to rates of failure substantially lower than the rates of exceedance of the design action" (fib 2012, p. 3).
"Risk-targeted maximum considered earthquake" (MCER) ground motion maps are a fairly new development in the United States. When using the previous uniform hazard maps, corresponding to a 2% probability of the ground motion being exceeded in 50 years, buildings were designed to resist uniform hazard ground shaking levels, whereas buildings designed by using the MCER maps are intended to provide the same level of seismic performance, meaning that they have the same risk level. According to Kircher et al. (2012), "The risk-targeted MCER ground motions are defined by two essential collapse objectives. First objective answers the question—what is the acceptable collapse risk, that is, what is the acceptable probability of collapse of a structure in 50 years? This probability was selected to be 1% (in 50 years) … The second collapse objective answers the question—what is the acceptable probability of collapse of a structure given the MCER ground motions occur at the site of interest? This conditional probability was selected to be 10% (given MCER ground motions). …. The 1% in 50-year collapse risk objective is the result of integrating the hazard function (which is different for each site) and the derivative of the "hypothetical" collapse fragility defined by the 10% conditional probability (and an appropriate amount of collapse uncertainty)." The new maps have been adopted in the 2010 edition of the ASCE 7 standard, and have remained in this standard also in the latest (ASCE 7-16) edition. However, many researchers and practicing engineers in United States are not happy with the new concept. There are several reasons for this. According to Hamburger, who is one of the key persons in the development of seismic codes in the United States, clients think they understand probabilistic ground motion (e.g. a 500-year or a 2500-year event), but do not understand designing for a ground motion that produces a 1% risk of collapse in 50 years. Most engineers do not understand this well either, and have a difficult time explaining it. Moreover, the 10% probability of collapse conditioned on MCER, which is the basis for design, seems to be too pessimistic given the very few collapses that have historically been experienced, mostly in a population of buildings that does not conform to the present code (RO Hamburger 2017, personal communication, 2. November 2017). The author and his colleagues have also some doubts about the concept of risk-targeted seismic maps. Whereas seismic hazard depends only on ground motion, risk depends both on ground motion and structural behaviour. The usual hazard maps are based solely on ground motion considerations, whereas the risk-targeted maps inevitably also involve structural considerations, which makes the process more complex and less transparent. The whole seismic design or assessment process is facilitated if the ground motion problems can be separated from the structural problems.
Performance-based earthquake engineering seeks to improve seismic risk decision-making through new design and assessment methods that have a probabilistic basis, as well as trying to take into account properly the inherent uncertainty. The goals of performance-based earthquake engineering can be achieved by using methods which allow for the explicit quantification of risk of collapse and of different damage states. Such procedures have already been developed. The most influential has been the work of Cornell and colleagues at Stanford University. In 1996, Cornell (1996a) published "a convenient explicit probabilistic basis for new seismic design and evaluation guidelines and codes". The proposed procedure avoided using "often very esoteric concepts of random vibration theory … or simulation of (practically) prohibitively large number of samples of events". Instead, "the proposed procedure makes use only of traditional and available tools". In the same year, Cornell (1996b) also presented his "personal view of the needs and possible future path of project-specific earthquake resistant design and re-assessment based on explicit reliability analysis" which "cannot be done without effective estimates of the likelihoods of loss- and injury-inducing structural behaviour". The procedure, proposed in Cornell (1996a), he classified as "future, but currently feasible, practice". In fact, the procedure became very popular among researchers. The well-known SAC-FEMA approach (Cornell et al. 2002) is based on this work. However, a procedure which requires a large number of NRHA analyses encounters difficulties when searching for a way into the codes.
In 2012, the Applied Technology Council (ATC) developed a methodology for the seismic performance assessment of buildings (FEMA P-58 2012). The technical basis of the methodology was the framework for performance based earthquake engineering developed by researchers at the Pacific Earthquake Engineering Research Center (PEER) between 1997 and 2010. As acknowledged in the Dedication of the report FEMA P-58, A. Cornell and H. Krawinkler were the leading forces in the development of this framework. The methodology is intended for use in a performance-based seismic design process. It is applicable to the assessment of new or existing buildings. The procedures are probabilistic, uncertainties are considered explicitly, and performance is expressed as the probable consequences, in terms of human losses (deaths and serious injuries), direct economic losses (building repair or replacement costs), and indirect losses (repair time and unsafe placarding) resulting from building damage due to earthquake shaking. The implementation of the methodology is described in companion volumes. An electronic Performance Assessment Calculation Tool (PACT) was also provided. Nevertheless, the comprehensive methodology has not yet been included in the codes.
A rigorous explicit probabilistic approach for structural analysis, which utilises recent research results, is, for example, the procedure provided in Appendix F to the FEMA P-695 document (2009). This methodology requires: (a) a structural model that can simulate collapse, (b) use of many (perhaps hundreds) of nonlinear response history analyses, and (c) explicit treatment of many types of uncertainties. "This process is too complex and lengthy for routine use in design." (Haselton et al. 2017). The explicit approach is nonetheless permitted by Section 1.3.1.3 (Performance-Based Procedures) of ASCE 7-10 and ASCE 7-16. Tables with target (acceptable, tolerable) reliabilities for failure were previously provided in the Commentary of ASCE 7-10, but have moved to the main part of the standard in ASCE 7-16. If using performance-based design, designers are supposed to demonstrate through testing and analysis that the design is capable of achieving these reliabilities. The analysis and design shall be "subject to the approval of the authority having jurisdiction for individual projects". However, the standard permits implicit demonstration that the target reliability can be achieved, therefore, in practice, explicit demonstration through calculation of a failure probability will almost certainly never be done (RO Hamburger 2017, personal communication, 2. November 2017). Moreover, Hamburger states: "I would not look to rapid adoption of these [explicit probabilistic] approaches procedures by the profession. Most engineers are not familiar with probability and statistics, let alone structural reliability theory. Most have a qualitative understanding of the basis for Load Resistance Factor Design, but are more than happy to assume that the load and resistance factors do what is necessary to give them safe designs."
In Europe, a very comprehensive document dealing with explicit probabilistic analysis is the Italian Guide for the Probabilistic Assessment of the Seismic Safety of Existing Buildings (CNR 2014), developed by P. E. Pinto and P. Franchin. The Guide is intended to "be of help in future revisions of the current standards". Three verification methods having different levels of complexity are presented.
In order to facilitate a gradual introduction of probabilistic considerations into practice and codes, highly simplified practice-oriented approaches for the determination of seismic risk are needed, at least as a first step. Very recently, an informative Annex to EC8, Part 1, entitled Simplified reliability-based verification format (CEN 2017), has been drafted by Dolšek et al. (2017b). It provides a basis for a simplified verification of the performance of a structure in probabilistic terms. It gives information about (a) a simplified reliability-based verification format; (b) a procedure for the estimation of the relationship between performance factors and the degree of reliability; and (c) a procedure for the estimation of behaviour (i.e. force reduction) factors with respect to target reliability for the NC limit state.
A very simple method called the Pushover-based Risk Assessment Method (PRA), which is in line with the Annex and which requires only a very minor effort in addition to a standard pushover-based analysis, is summarized in the next section. For more details, see Kosič et al. (2017), Dolšek and Fajfar (2007) and Fajfar and Dolšek (2012). By combining Cornell's closed form solution (Cornell 1996a) and the pushover-based N2 method (Fajfar 2000), which is used for the determination of the capacity of the structure, the annual probability of "failure" of a structure can be easily estimated, provided that predetermined default values for dispersions are available. Compared to Cornell's original approach, in the PRA method a large number of nonlinear response history analyses is replaced by a few pushover analyses (in most cases just a single one). Of course, like other simplified methods, the PRA method has limitations, which are basically the same as those which apply to Cornell's closed form solution and to the basic N2 method.
Summary of the pushover-based risk assessment (PRA) method
The "failure" probability of building structures, i.e. the annual probability of exceeding the near collapse limit state (NC), which is assumed to be related to a complete economic failure of a structure, can be estimated (Cornell 1996a; Fajfar and Dolšek 2012; Kosič et al. 2017) as:
$$P_{f} = P_{NC} = \exp \left[ {0.5k^{2} \beta_{NC}^{2} } \right]{\kern 1pt} H(S_{aNC} ) = \exp \left[ {{\kern 1pt} 0.5k^{2} \beta_{NC}^{2} } \right]k_{0} S_{aNC}^{ - k} ,$$
(1)
where S aNC is the median NC limit state spectral acceleration at the fundamental period of the structure (i.e. the capacity at failure), and β NC is the dispersion measure, expressed as the standard deviation of the natural logarithm of S aNC due to record-to-record variability and modelling uncertainty. The parameters k and k 0 are related to the hazard curve H(S a ) which is assumed to be linear in the logarithmic domain
$$H(S_{a} ) = k_{0} S_{a}^{ - k} .$$
(2)
A seismic hazard curve shows the annual rate or probability at which a specific ground motion level will be exceeded at the site of interest. The reciprocal of the annual probability of exceedance is the return period T R = 1/H.
In principle, dispersion β NC and hazard function should be consistent with the intensity measure S a , since they depend on it.
The capacity at failure S aNC is estimated using the pushover-based N2 method (Fajfar 2000), whereas predetermined dispersion values are used for β NC . Note that, in principle, Eq. (1) can be applied for any limit state, provided that the median value and the dispersion of the selected intensity measure are related to the selected limit state. A widely accepted definition of the NC limit state, referred to in this paper also as "failure", is still not available. One possibility is to relate the global NC limit state to the NC limit state of the most critical vertical element. Another option is to assume that the NC limit state corresponds to 80% strength at the softening branch of the pushover curve. The NC limit state was selected instead of the C (collapse) limit state, since it is much easier to estimate capacities for the NC limit state than for the C limit state. It should be noted, however, that the tolerable probabilities of exceedance are higher for the NC than for the C limit state.
The determination of the spectral acceleration at the NC limit state S aNC can be visualized in Fig. 6, where the equal displacement rule is assumed. In the acceleration–displacement (AD) format, S aNC is defined by the crossing point of the vertical line, representing the displacement at the NC limit state, i.e. the displacement capacity of the equivalent single-degree-of-freedom system representing the structure, and the diagonal line, representing the period of the structure. The crossing point is a point on the acceleration spectrum, which corresponds to the NC level ground motion.
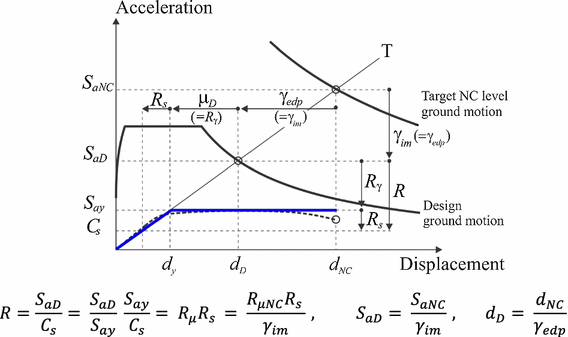
Illustration of parameters relevant for the determination of the capacities and force reduction factors. In the plot the validity of the equal displacement rule was assumed. The presented parameters apply to a general case, with the exception of the equalities in brackets which apply only in the case if the equal displacement rule is valid
Full size image
According to Eq. (1), the failure probability is equal to the hazard curve evaluated at the median capacityS aNC , multiplied by an exponential magnification factor which depends on the product of the variability of the S aNC (expressed by β NC ) and the slope (in log–log terms) k of the hazard curve. For frequently used values (β NC = 0.5 and k = 3.0) the correction factor amounts to 3.1. In such a case the probability of failure is about three times larger than the probability of the exceedance of the ground motion corresponding to the median capacity at failure in terms of the spectral acceleration S aNC . If there was no variability (β NC = 0), both probabilities would be equal.
Extensive studies have been performed in order to determine typical dispersions β NC of the capacity at failure for reinforced concrete (RC) building structures using S a (T) as the intensity measure (Kosič et al. 2014, 2016). The results of these studies showed that the values depend on the structural system and on the period of the structure T. However, in a simplified approach, it may be reasonable to assume \(\beta_{NC} = 0. 5\) as an appropriate estimate for RC building structures, with the exception of very stiff structures, where \(\beta_{NC}\) is smaller. This value takes into account both aleatory (related to ground motion) and epistemic (related to structural modelling) uncertainty.
Several options are available for the estimation of the parameters k and k 0. Best k and k 0 estimates can be obtained by fitting the actual hazard curve by a linear function in logarithmic domain. In absence of an appropriate hazard curve, k can be estimated from seismic hazard maps for two return periods. If hazard maps for two different return periods are not available, the only (very approximate) option is to assume a value of k depending on the geographical location of the structure. Appropriate values of k are usually within the range from 1 to 3 (exceptionally to 4). If the value of k, specific for the region, is not known, a value of k = 3.0 has often been used as an option in high seismicity regions. In low seismicity regions the k values are usually smaller. Note that k also depends on the intensity measure used in Eq. (1). In the case of the spectral acceleration S a , it depends on the period of the structure. This dependence should be taken into account when a more accurate analysis is being sought (Dolšek et al. 2017a).
For the determination of the parameter k 0 at least one value of S a , corresponding to a specific return period needs to be known for the location under consideration, e.g. S aD that corresponds to the return period of the design ground motion T D and represents the spectral acceleration in the elastic design spectrum. Knowing the value S aD and the corresponding annual frequency of exceedance (H = 1/T D ), the parameter k 0 can be obtained from Eq. (2) as follows:
$$k_{0} = 1/(T_{D} \cdot S_{aD}^{ - k} ).$$
(3)
Considering Eq. (3), Eq. (1) can be written in the form
$$P_{NC} = \exp {\kern 1pt} \left[ {{\kern 1pt} 0.5k^{2} \beta_{NC}^{2} } \right]\frac{1}{{T_{D} }}\left( {\frac{{S_{aNC} }}{{S_{aD} }}} \right)^{ - k} .$$
(4)
Applications of the PRA method
The results of extensive studies have demonstrated that the PRA method has the potential to predict the seismic risk of low- to medium-rise building structures with reasonable accuracy, so it could become a practical tool for engineers. Typical values of probabilities of exceedance of the NC limit state in a life-span of 50 years are, in the case of buildings designed according to modern codes, about 1%. In the case of older buildings, not designed for seismic resistance, the probabilities are usually at least one order of magnitude higher (see, e.g., Kosič et al. 2014, 2016). It should be noted, however, that the absolute values of the estimated failure probability are highly sensitive to the input data and simplifying assumptions, especially those related to the seismic hazard. Comparisons between different structures are more reliable. Comparative probabilistic analyses can provide valuable additional data necessary for decision-making. Due to its simplicity, the PRA method can also serve as a tool for the introduction of explicit probabilistic considerations into structural engineering practice.
The basic equation for the probability of failure can also be used in risk-targeted design. In recent years this issue has been intensively studied by M. Dolšek and his PhD students. Already in 2014, Žižmond and Dolšek (2014) prepared a manuscript proposing "risk-targeted behaviour factor". In that manuscript the concept of force reduction factors based on acceptable risk was developed and formulated in a form very similar to Eq. (12). The idea and the formulation, originally presented in that manuscript, are of great help for understanding the empirical values of force reduction factors and allow a scientifically based quantification of these factors. Unfortunately, that manuscript was not accepted for publication in the international journal to which it was submitted. A very substantial part of the text which follows in this section is based on the work, ideas and formulations of M. Dolšek and his former students, especially J. Žižmond and N. Lazar Sinković.
For design purposes, Eq. (4) has to be inverted in order to express the ratio between the spectral acceleration at failure S aNC and the design spectral acceleration S aD as a function of the return period corresponding to the target probability of failure T NC = 1/P NC and the parameters k and β NC
$$\frac{{S_{aNC} }}{{S_{aD} }} = \left( {\frac{{T_{NC} }}{{T_{D} }}} \right)^{{\frac{1}{k}}} \exp \left[ {{\kern 1pt} 0.5k\beta_{NC}^{2} } \right] = \gamma_{im} ,$$
(5)
where index im stands for Intensity Measure (i.e. spectral acceleration at the fundamental period of the structure).
The factor γ im , initially proposed by Žižmond and Dolšek (2014, 2017), further elaborated in Dolšek et al. (2017a), and used also in the draft Annex to revised EC8 (Dolšek et al. 2017b; CEN 2017), is the product of two factors.
The first factor ((T NC /T D )1/k ) takes into account the fact that the target probability of failure (the NC limit state) is smaller than the probability of the design ground motion or, expressed in terms of return periods, the target return period of failure is larger than the return period of design ground motion. For example, in EC8 the design ground motion for common structures corresponds to a return period of 475 years and is related to the significant damage (SD) limit state. Although the SD limit state is not well defined, it certainly corresponds to a much smaller damage than the NC limit state. It is attained at a much smaller deformation. The value of this factor is equal to 1.0 if T NC =T D .
The second factor takes into account the uncertainties both in the ground motion (record to record dispersion) and in the modelling. In codes, safety factors, which take into account possible less favourable conditions, should be used. Safety factors are typically based on probabilistic considerations and on experience. In a standard deterministic analysis, the fixed values prescribed in codes are used. If a probabilistic analysis is used, the uncertainty can be explicitly included in the calculations. The value of this term is 1.0 if β NC = 0, i.e. if there is no uncertainty. Note that the second factor is similar to the magnification factor in Eq. (1), the difference is only in the exponent of k (1 vs. 2).
The factor γ im depends on the target and design return period, on the slope of the hazard curve k, and on the dispersion β NC . For some frequently used input data (k = 3, β NC = 0.5, T NC = 5000 years, T D = 475 years), γ im = 2.19 × 1.46 = 3.20.
By analogy to Eq. (5), the ratio of displacements d NC /d D , can be written as:
$$\frac{{d_{NC} }}{{d_{D} }} = \gamma_{edp} ,$$
(6)
where the index edp stands for Engineering Demand Parameter (Dolšek et al. 2017a).
If the equal displacement rule applies, the ratio of accelerations is equal to the ratio of displacements (Fig. 6) so that both \(\gamma\) values are equal:
$$\gamma_{edp} = \gamma_{im} .$$
(7)
If the equal displacement rule does not apply, e.g. in the case of buildings with fundamental period in the short period range, a more general relation between the two \(\gamma\) factors can be derived, provided that the relationship between the spectral acceleration and displacement, i.e. between im and edp, is defined in closed form. Using the simple R–μ–T relationship (Fajfar 2000), implemented in EC8, Dolšek et al. (2017a) derived a relation for structures with short periods, i.e. for structures with the fundamental period T less than the characteristic period of the ground motion T C :
$$\gamma_{edp} = \frac{{\left( {\gamma_{im} \frac{{S_{aD} }}{{S_{ay} }} - 1} \right)\frac{{T_{C} }}{T} + 1}}{{\left( {\frac{{S_{aD} }}{{S_{ay} }} - 1} \right)\frac{{T_{C} }}{T} + 1}},$$
(8)
where S ay represents the acceleration at the yield point of the structure (Fig. 6).
Dolšek et al. (2017a) called both γ factors "risk-targeted safety factors", since they depend, inter alia, on the selected acceptable collapse risk. γ edp can be used, for example, in displacement-based design for determining the displacement capacity, whereas γ im can be applied when determining the force reduction factors used in force-based design, as explained in the text which follows. In both cases, the γ factors should be applied to "best estimate" values, i.e. values determined without any partial safety factors.
In the case of the nonlinear analysis in EC8, the design ground motion corresponds to a return period of 475 years, whereas the target return period for failure (the NC limit state) is much larger. The deformation demand, determined for a 475 year return period, cannot be directly compared with the median deformation capacity corresponding to the NC limit state. In order to allow a direct comparison of demand and capacity with proper consideration of safety, the median NC capacity in terms of displacements has to be reduced by dividing the NC displacement capacity with the risk-targeted safety factor γ edp , which takes into account both the difference in return periods and dispersion. Earlier in this section it was shown that, for some frequently used data, γ im is equal to about 3. For structures with the fundamental period in the moderate or long period range, for which the equal displacement rule applies, γ edp is equal to γ im . Thus, in such a case the displacement capacity to be compared with the displacement demand, i.e. the design displacement capacity, should be about three times smaller than the NC displacement capacity. For more details see (Dolšek et al. 2017a).
Using the idea and formulation of Žižmond and Dolšek (2014, 2017), the risk-targeted safety factor γ im can be used for the determination of the risk-targeted force reduction factor R, as shown in the text which follows.
The force reduction factor R can be presented as a product of two factors:
$$R = R_{\mu } \cdot R_{s} ,$$
(9)
where R s is the so-called overstrength factor, and R μ is the reduction factor component which takes into account the deformation capacity and the inelastic dissipation energy capacity. R μ is also called ductility dependent part of the R factor. The overstrength factor, which is an inherent property of properly designed, detailed, constructed and maintained highly redundant structures, is defined as the ratio between the actual strength of the structure and the strength used in code design. R μ is usually expressed in terms of a ductility factor, i.e. the ratio between the deformation capacity (usually displacements) and the deformation at yield. In general, it depends on the period of the structure T. If the equal displacement rule applies, the ductility dependent R μ factor is equal to the ductility factor:
$$R_{\mu } = \mu .$$
(10)
In other cases, e.g. in the case of stiff structures with short periods, other relations are used, e.g. the simple relation (Fajfar 2000), implemented in EC8:
$$R_{\mu } = (\mu - 1)\frac{T}{{T_{C} }} + 1,\quad T < T_{C}$$
(11)
where T C is the characteristic period of ground motion.
When determining the value of a force reduction factor to be used in a code, it is of paramount importance to take into account an appropriate value of the displacement and ductility, which control the ductility dependent part of the reduction factor R μ . The difference between the return period of the design ground motion and the target return period of failure has to be taken into account, as well as uncertainties. This can be achieved by using the design displacement capacity, as defined in the previous example of application, i.e. the median displacement capacity at failure (the NC limit state) divided by the factor γ edp . Alternatively, if the median NC displacement capacity is used for the determination of the factor R μ (denoted as R μNC ), the force reduction factor according to Eq. (9) should be reduced by the factor γ im (Žižmond and Dolšek 2014, 2017; Dolšek et al. 2017b; CEN 2017):
$$R = \frac{{R_{\mu NC} \cdot R_{s} }}{{\gamma_{im} }}$$
(12)
The different parameters which are related to the force reduction factor are illustrated in Fig. 6. The presentation of the parameters is similar to that in Fig. 1–2 presented in FEMA P-695 (FEMA 2009). The parameters (with the exception of accelerations and displacements at both axes which have dimensions) are dimensionless ratios of accelerations or displacements. They are depicted as the differences between two related parameters rather than as ratios of the parameters. In order to facilitate presentation, in the plot the validity of the equal displacement rule was assumed. Nevertheless, the presented parameters apply to a general case, with the exception of the equalities in brackets which apply only in the case if the equal displacement rule is valid. C s is the seismic coefficient, i.e. the reduced acceleration used for the determination of design seismic action.
Equation (9) has often been used for the determination of force reduction factors from the results of experimental and numerical investigations. Recently, many studies have been aimed at determining appropriate values of reduction factors, e.g. FEMA P-695 (2009). This study, which took into account probabilistic considerations, is an example of a correct procedure. On the other hand, there have been some studies aimed at determining force reduction factors for specific structural systems, in which Eq. (9) was used incorrectly, i.e. too large values of the ductility dependent R μ factor were applied.
The principle of the reduction of forces and the derivation of relevant equations, shown in the previous text, is based on a single-degree-of-freedom (SDOF) system. Nevertheless, the force reduction factor approach has been widely used in codes also for multi-storey buildings modelled as multi-degree-of-freedom (MDOF) systems which can be approximately represented by an equivalent SDOF system.
Tolerable probability of failure
General
When determining the tolerable (called also acceptable or target) probability of failure, the possible consequences in terms of risk to life and injury, the potential economic losses, and the likely social and environmental effects need be taken into account. The choice of the target level of reliability should also take into account the amount of expense and effort required to reduce the risk of failure. The acceptable risk is, of course, a reflection of personal and societal value judgements, as well as disaster-based experience, and differs from one cultural environment to another. It is therefore no wonder that generally accepted quantitative values for target structural reliability, which could possibly be used in seismic design, do not exist. Nevertheless, some data are provided in the existing seismic regulations, as discussed in the text which follows.
The standard measures for structural reliability are the reliability index β and the probability of failure P f , both of which are expressed either at the annual level or for the reference period of the expected working life of the structure (50 years in the case of ordinary buildings). The relationship between the probability of failure and the reliability index is given as:
$$P_{f } = \Phi ( - \,\beta )$$
(13)
where Φ(·) is the standard normal cumulative probability distribution function. Numerical values of the β −P f relationship are given in Table 2.
Full size table
The reliability index β should not be confused with the dispersion measure β which is used in Sects. 4.3 and 4.4.
In EN 1990 (also referred to as Eurocode 0, CEN 2002) the target reliability depends on the consequence class, i.e. on the consequences of the potential failure of buildings. For ordinary buildings, the target reliability index for the "ultimate limit state" related to 1-year reference period is equal to β = 4.7 (the same value as that in the ISO 13822 standard). The corresponding probability of failure is about P f ≈ 10−6. In Sect. 2.2 of EN 1990 it is stated that the choice of the levels of reliability should take into account, in addition to the consequences of failure, also "the expense and procedures necessary to reduce the risk of failure". However, the provided target reliability indices do not depend on cost issues. In the draft of the revised EN 1990, which is at the development stage, the target annual probability of failure P f ≈ 10−6 remained unchanged. However, it is explicitly stated that seismic limit states are excluded.
In the fib model code (2010), Section 3.3.3 is related to reliability. As in EN 1990, it is stated that the target level of reliability should take into account the possible consequences as well as the amount of expense and effort required to reduce the risk of failure. It is also stated that due attention should be paid to differentiating the reliability level of new and existing structures, since the costs of increasing the safety of existing structures are usually high compared to the costs for new structures. Such a differentiation of the reliability level can be performed on the basis of a "well founded analysis". If such an analysis is omitted, recommended target reliability indices can be used. The target reliabilities for ordinary buildings are the same as those given in EN 1990. In the case of recommended values, no distinction is made with regard the costs of safety measures.
The Probabilistic model code (JCSS 2000) provides target reliability indices which depend not only on the consequences of failure but also on the relative cost of safety measures. In the code (p. 18), it is stated: "A large uncertainty in either loading or resistance (coefficients of variation larger than 40%), as for instance the case of many accidental and seismic situations, a lower reliability class should be used. The point is that for these large uncertainties the additional costs to achieve a high reliability are prohibitive." For ordinary buildings and normal relative costs of safety measures, a reliability index for 1 year β = 4.2 (P f ≈ 10−5) is used, whereas in the case of large costs (typical for seismic protection) β = 3.3 (P f ≈ 5 × 10−4). In the model code, it is also stated that failure consequences also depend on the type of failure, which can be ductile or brittle. "A structural element which would be likely to collapse suddenly without warning should be designed for a higher level of reliability than one for which a collapse is preceded by some kind of warning which enables measures to be taken to avoid severe consequences." (JCSS 2000).
The target probabilities of failure in all three codes, which do not take into account the difference in cost needed for increasing safety in a seismic design situation compared to standard design, are much lower than that which could possibly be achieved by complying with the current seismic codes. Only if the differentiation of the reliability index according to the cost of safety measures is made, as suggested in all three codes, but realized in the form of reduced target reliability indices only in the case of the Probabilistic model code, the target probabilities are increased to more realistic values. The annul probability P f ≈ 5 × 10−4 (2.5% in 50 years), provided in the Probabilistic model code for ordinary buildings, is even substantially higher than the currently most popular value P f = 2 × 10−4 (1% in 50 years, β ≈ 3.5), suggested also in the draft Annex to the revised EC8 (CEN 2017; Dolšek et al. 2017b), and confirmed in a discussion among European code developers. The latter value is comparable to the probabilities of failure estimated for buildings compliant with current seismic codes.
In ASCE 7-16 reliability indices for "load conditions that do not include earthquake, tsunami, or extraordinary events" are provided. For "structural stability caused by earthquake", target reliabilities are given in terms of "conditional probability of failure caused by the MCER shaking hazard". For ordinary buildings the target probability amounts to 10%. (For discussion on the MCER concept, see Sect. 4.2.) It should be noted that the conditional probability of failure due an assumed earthquake cannot be directly compared with the probability of failure due to earthquakes in the working life of a building.
When discussing acceptable risk of failure, a distinction should be made between physical collapse (i.e. the collapse or C limit state) and economic failure without physical collapse (i.e. the near collapse or NC limit state). Of course, the tolerable probability for collapse, which would very likely result in human casualties, is smaller. Apparently, the definition of failure in most codes corresponds to the NC limit state. In EN 1990 it is stated: "States prior to structural collapse, which, for simplicity, are considered in place of the collapse itself, may be treated as ultimate limit states." Also the estimation of seismic risk in probabilistic analyses is mostly related to the NC limit state, since it is extremely difficult to numerically simulate the complete physical collapse of a building.
Acceptable risk in Slovenia
The Republic of Slovenia is a country with a moderate seismic hazard, where earthquakes up to a magnitude of about 7 and an EMS intensity of IX are possible throughout its territory. An internet-based survey was conducted in 2013 in order to gather data about the perception of seismic risk in Slovenia. In view of the expected differences of opinion between experts and the lay public, the survey was conducted in two groups, where respondents were differentiated according to their expertise in the field of project design and building construction. The first group of respondents were members of the Slovenian Chamber of Engineers (denoted as "experts"). 217 responses were received. Most of the respondents were working in the field of project design (55%) or construction (41%). Their answers were compared to the answers of the lay public sample (502 respondents) which was located using snowball sampling. It should be noted that the sample of lay people was not representative for all inhabitants of Slovenia, and was to a large extent limited to people with higher levels of education. The results of the survey did not, in most cases, show significant differences between the two samples. High agreement between the answers was observed also in the answers regarding the tolerable probability of collapse of buildings built according to the current seismic regulations. Both groups were asked how many buildings, on average, can be tolerated to collapse as a direct consequence of an earthquake during their expected working life (i.e. 50 years). The results are shown in Fig. 7(left). In a similar question respondents were asked about the tolerable probability of economic failure (i.e. the building does not collapse physically, but repair is not economically justified, corresponding to the NC limit state) for buildings built according to the current seismic regulations (Fig. 7, right)]. A significantly higher tolerable probability than in the case of building collapse was expected. However, surprisingly, there was only a small difference between the tolerable probability of collapse and the tolerable probability of economic failure. For both groups of respondents, a large scatter of results can be observed. The mean values of the tolerable probabilities of collapse and economic failure in a working life of 50 years are presented in Table 3. More details of the survey are available in Fajfar et al. (2014).
Distribution of tolerable probabilities of collapse and economic failure in 50 years for ordinary buildings, built according to the current seismic regulations
Full size image
Full size table
The results shown in Table 3 suggest that both experts and lay people expect, on average, a lower probability of failure than that which has been estimated for buildings complying with the current seismic regulations.
Conclusions: analysis procedures available for all needs
The seismic response of structures subjected to strong ground motion is dynamic, inelastic, and random. Historically, the three major response characteristics of seismic structural response have only gradually penetrated into the analysis of structures, which is one of the most important parts of seismic provisions. Such analysis provides estimates of seismic demands, which are then compared with corresponding capacities.
After static analysis, which was used in early codes, linear dynamic methods were developed and are currently well established. Explicit nonlinear analysis, taking into account inelastic structural behaviour, is a relatively new achievement. In recent seismic codes, explicit nonlinear analysis has been typically adopted as an optional procedure, which, however, is in some codes mandatory for special structural systems. The most advanced deterministic analysis method available today is nonlinear response history analysis (NRHA). It is irreplaceable for the research and for the design and/or assessment of very important buildings. However, due to its complexity, it has, in practice, only rarely been used, with the exception of some special structures. Pushover-based methods are a simpler option, combining a nonlinear static (pushover) analysis with the response spectrum approach. They represent a rational practice-oriented tool for the seismic analysis of many but not all structures.
Probabilistic considerations have been taken into account in seismic hazard analysis and in the development of different kinds of safety factors, whereas an explicit probabilistic approach, which allows a quantification of risk, as needed in performance-based earthquake engineering, has not yet been implemented in seismic building codes, with the partial exception of the United States. Considering the reluctance of the great majority of engineers and also a large part of researchers to accept probabilistic methods, it is extremely unlikely that these methods will be adopted in seismic codes in the foreseeable future as a mandatory option. They are indispensable, however, for a better calibration of different safety factors and force reduction factors in current codes.
A rigorous seismic analysis that could take into account all three major response characteristics (dynamics, inelasticity and randomness) is too demanding for most practical applications. As well as this, the large uncertainties which are related to both ground motion and the modelling of structures do not permit accurate predictions of the structural response during future earthquakes. Simplified approaches have been developed in different historical periods, depending on the knowledge and computational tools available at the time. When a new procedure was implemented, the existing analysis procedures mostly remained in the codes. For example, dynamic analysis has not replaced static analysis, and nonlinear analysis has not replaced linear analysis; the new procedures just complemented the old ones. Currently, several analysis procedures with different complexity levels are available for different needs. They have been developed to a stage in which, if properly applied, permit, together with appropriate conceptual design, dimensioning and detailing, the construction of building structures which, with a very high probability, would not collapse due to earthquakes. This has been often demonstrated in recent earthquakes. Unfortunately, the limitation of structural and non-structural damage is still an issue. Further improvements are needed, inter alia, in the reliability of input data and structural modelling. In practice, the competence of designers, as well as the financial and time restrictions imposed on the design projects, also have to be taken into account.
References
-
Army (1986) Seismic design guidelines for essential buildings. Departments of the Army (TM 5-809-10-1), Navy (NAVFAC P355.1), and the Air Force (AFM 88-3, Chapter 13, Section A), Washington, DC
-
ASCE (2014) Seismic evaluation and retrofit of existing buildings, ASCE/SEI 41-13. American Society of Civil Engineers, Reston
Book Google Scholar
-
ASCE (2017) Minimum design loads and associated criteria for buildings and other structures, ASCE/SEI 7-16. American Society of Civil Engineers, Reston
Google Scholar
-
ATC (1978) Tentative provisions for the development of seismic regulations for buildings, ATC 3-06. National Bureau of Standards, Washington
Google Scholar
-
ATC (1995) Structural response modification factors, ATC-19. Applied Technology Council, Redwood City
Google Scholar
-
ATC (1996) Seismic evaluation and retrofit of concrete buildings (Report SSC 96-01 of California Seismic Safety Commission). Report ATC-40. Applied Technology Council, Redwood City, CA
-
Aydinoğlu MN, Önem G (2010) Evaluation of analysis procedures for seismic assessment and retrofit design. In: Garevski M, Ansal A (eds) Earthquake engineering in Europe, vol 17. Geotechnical, geological and earthquake engineering. Springer, Dordrecht, pp 171–198
Chapter Google Scholar
-
Baros D, Anagnostopoulos SA (2008) An assessment of static non-linear pushover analyses in 2-D and 3-D applications. In: Bento R, Pinho R (eds) 3D pushover 2008—nonlinear static methods for design/assessment of 3D structures. IST press, Lisbon
Google Scholar
-
Berg GV (1983) Seismic design codes and procedures. Earthquake Engineering Research Institute, Berkeley
Google Scholar
-
Bertero VV (2009) Vitelmo V. Bertero. In: Reitherman R (interviewer) Connections: EERI oral history series. Earthquake Engineering Research Institute, Oakland, CA
-
Blume JA, Newmark NM, Corning LH (1961) Design of multistory reinforced concrete buildings for earthquake motions. Portland Cement Association, Chicago
Google Scholar
-
Cardoso R, Lopes M, Bento R (2004) Earthquake resistant structures of Portuguese old 'Pombalino' buildings. In: Proceedings of the 13th world conference on earthquake engineering, Paper No. 918, Vancouver, BC, Canada
-
CEN (2002) European standard EN 1990:2002. Eurocode: basis of structural design. European Committee for Standardization, Brussels
Google Scholar
-
CEN (2004) European standard EN 1998-1:2004, Eurocode 8: design of structures for earthquake resistance, part 1: general rules, seismic action and rules for buildings. European Committee for Standardization, Brussels
Google Scholar
-
CEN (2017) Draft Annex F (Informative): simplified reliability-based verification format, Annex to European standard EN 1998–1. Eurocode 8: design of structures for earthquake resistance. Part 1: general rules, seismic action and rules for buildings. European Committee for Standardization. Brussels (Prepared by Dolšek M, Žižmond J, Kosič M, Lazar Sinković N)
-
Chopra AK (2007) Elastic response spectrum: a historical note. Earthq Eng Struct Dyn 36:3–12
Article Google Scholar
-
Chopra AK (2017) Dynamics of structures: theory and applications to earthquake engineering, 5th edn. Pearson, Hoboken
Google Scholar
-
Chopra AK, Goel RK (2002) A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq Eng Struct Dyn 31(3):561–582
Article Google Scholar
-
Chopra AK, Goel RK, Chintanapakdee C (2004) Evaluation of a modified MPA procedure assuming higher modes as elastic to estimate seismic demands. Earthq Spectra 20(3):757–778
Article Google Scholar
-
Clough R (1980) The finite element method after twenty-five years: a personal view. Comput Struct 12(4):361–370
Article Google Scholar
-
CNR (2014) Guide for the probabilistic assessment of the seismic safety of existing buildings, Report CNR-DT 212/2013. CNR—Advisory Committee on Technical Recommendations for Construction, Rome
-
Cornell CA (1996a) Calculating building seismic performance reliability: a basis for multi‐level design norms. In: Proceedings of the 11th world conference on earthquake engineering, Mexico City, Mexico, Paper No. 2122
-
Cornell CA (1996b) Reliability-based earthquake-resistant design: the future. In: Proceedings of the 11th world conference on earthquake engineering, Mexico City, Mexico, Paper No. 2166
-
Cornell CA, Jalayar F, Hamburger RO, Foutch DA (2002) Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines. J Struct Eng ASCE 128(4):526–533
Article Google Scholar
-
Deierlein GG, Reinhorn AM, Wilford MR (2010) Nonlinear structural analysis for seismic design. A guide for practicing engineers. NEHRP seismic design technical brief No. 4, NIST GRC 10-917-5. National Institute of Standards and Technology, Gaithersburg, MD
-
Diebold J, Moore K, Hale T, Mochizuki G (2008) SEAOC Blue Book: seismic design recommendations 1959 to 2008. In: Proceedings of the 14th world conference on earthquake engineering, Beijing, China
-
Dolšek M, Fajfar P (2007) Simplified probabilistic seismic performance assessment of plan-asymmetric buildings. Earthq Eng Struct Dyn 36(13):2021–2041
Article Google Scholar
-
Dolšek M, Lazar Sinković N, Žižmond J (2017a) IM-based and EDP-based decision models for the verification of the seismic collapse safety of buildings. Earthq Eng Struct Dyn 36(15):2665–2682
Google Scholar
-
Dolšek M, Žižmond J, Kosič M, Lazar Sinković N (2017b) Simplified reliability-based verification format, working material for Annex F to revised EN 1998-1. University of Ljubljana, Ljubljana
Google Scholar
-
Fajfar P (1999) Capacity spectrum method based on inelastic demand spectra. Earthq Eng Struct Dyn 28:979–993
Article Google Scholar
-
Fajfar P (2000) A nonlinear analysis method for performance-based seismic design. Earthq Spectra 16(3):573–592
Article Google Scholar
-
Fajfar P, Fischinger M (1987) Non-linear seismic analysis of RC buildings: implications of a case study. Eur Earthq Eng 1:31–43
Google Scholar
-
Fajfar P, Fischinger M (1989) N2—a method for non-linear seismic analysis of regular buildings. In: Proceedings of the 9th world conference on earthquake engineering, Tokyo, Kyoto, 1988, Maruzen, Tokyo, vol V, pp 111–116
-
Fajfar P, Dolšek M (2012) A practice-oriented estimation of the failure probability of building structures. Earthq Eng Struct Dyn 41(3):531–547
Article Google Scholar
-
Fajfar P, Marušić D, Peruš I (2005) Torsional effects in the pushover-based seismic analysis of buildings. J Earthq Eng 9(6):831–854
Google Scholar
-
Fajfar P, Polič M, Klinc R (2014) Perception of seismic risk by experts and lay people. Gradbeni vestnik 63:111–118 (in Slovenian)
Google Scholar
-
Fardis MN, Carvalho EC, Fajfar P, Pecker A (2015) Seismic design of concrete buildings to Eurocode 8. CRC Press, Boca Raton
Google Scholar
-
FEMA (1997) NEHRP guidelines for the seismic rehabilitation of buildings, FEMA 273. Federal Emergency Management Agency, Washington
Google Scholar
-
FEMA (2009) Quantification of Building Seismic Performance Factors, FEMA P-695. Federal Emergency Management Agency, Washington
Google Scholar
-
FEMA (2012) Next-generation methodology for seismic performance assessment of buildings, prepared by ATC for FEMA, FEMA P-58. Federal Emergency Management Agency, Washington
Google Scholar
-
fib (2010) Model code. International Federation for Structural Concrete, Lausanne, Switzerland
-
fib (2012) Probabilistic performance-based seismic design. Technical report prepared by Task Group 7.7. International Federation for Structural Concrete, Lausanne, Switzerland
-
Fischinger M, Isaković T, Fajfar P (2015) Yugoslav seismic code JUS 31/81 and Eurocode 8—a tribute to the IZIIS contribution towards development of the modern EU seismic standards. In: Proceedings of the international conference on earthquake engineering and seismology IZIIS50. Institute of Earthquake Engineering and Engineering Seismology, Skopje, Macedonia
-
Freeman JR (1930) Engineering data needed on earthquake motion for use in the design of earthquake-resisting structures. In: Proceedings of the 1930 meeting of the Eastern section of the seismological Society of America. U.S. Bureau of Standards, Washington, DC
-
Freeman JR (1932) Earthquake damage and earthquake insurance. McGraw-Hill, New York
Google Scholar
-
Freeman SA, Nicoletti JP, Tyrell JV (1975) Evaluations of existing buildings for seismic risk—a case study of Puget Sound naval shipyard, Bremerton, Washington. In: Proceedings of the U.S. national conference on earthquake engineering, Berkeley, CA, pp 113–122
-
Haselton CB, Baker JW, Stewart JP, Whittaker AS, Luco N, Fry A, Hamburger RO, Zimmerman RB, Hooper JD, Charney FA, Pekelnicky RG (2017) Response history analysis for the design of new buildings in the NEHRP provisions and ASCE/SEI 7 standard: part I—overview and specification of ground motions. Earthq Spectra 33(2):373–395
Article Google Scholar
-
Housner GW (1984) Historical view of earthquake engineering. In: Proceedings of the 8th world conference on earthquake engineering, post-conference volume: 25–39. San Francisco, CA
-
JCSS (2000). Probabilistic model code—part 1: basis of design. Joint Committee on Structural Safety
-
Jiang H, Lu X, Zhu J (2012) Performance-based seismic analysis and design of code-exceeding tall buildings in Mainland China. Struct Eng Mech 43(4):545–560
Article Google Scholar
-
JUS (1981) Code of technical regulations for the design and construction of buildings in seismic regions. Official Gazette of SFR Yugoslavia, 31/81 (English translation in Earthquake resistant regulations, a world list—1992, IAEE)
-
Kircher CA, Harris JL, Heintz JA, Hortacsu A (2012) ATC-84 project: improved seismic performance factors for design of new buildings. In: Proceedings of the 10th U.S. national conference on earthquake engineering, Anchorage, AK
-
Korčinski IL (1964) Fundamentals of design of buildings in seismic. Gradjevinska knjiga, Beograd (translation, original in Russian 1961) (in Serbian)
-
Kosič M, Fajfar P, Dolšek M (2014) Approximate seismic risk assessment of building structures with explicit consideration of uncertainties. Earthq Eng Struct Dyn 43(10):1483–1502
Article Google Scholar
-
Kosič M, Dolšek M, Fajfar P (2016) Dispersions for pushover-based risk assessment of reinforced concrete frames and cantilever walls. Earthq Eng Struct Dyn 45(13):2163–2183
Article Google Scholar
-
Kosič M, Dolšek M, Fajfar P (2017) Pushover-based risk assessment method: a practical tool for risk assessment of building structures. In: Proceedings of the 16th world conference on earthquake engineering, Santiago, Chile
-
Krause G (2014) Erdbebensicheres Bauen im Spanischen Weltreich, DGG- Mitteilungen 2/2014: 14-15, Deutsche Geophysikalische Gesellschaft e.V. ISSN 0934-6554 DGG
-
Krawinkler H (2006) Importance of good nonlinear analysis. Struct Des Tall Spec Build 15(5):515–531
Article Google Scholar
-
Krawinkler H, Seneviratna GDPK (1998) Pros and cons of a pushover analysis for seismic performance evaluation. Eng Struct 20(4–6):452–464
Article Google Scholar
-
Kreslin M, Fajfar P (2011) The extended N2 method taking into account higher mode effects in elevation. Earthq Eng Struct Dyn 40(14):1571–1589
Article Google Scholar
-
Kreslin M, Fajfar P (2012) The extended N2 method considering higher mode effects in both plan and elevation. Bull Earthq Eng 10(2):695–715
Article Google Scholar
-
Mahaney JA, Paret TF, Kehoe BE, Freeman SA (1993) The capacity spectrum method for evaluating structural response during the Loma Prieta earthquake. In: Proceedings of 1993 national earthquake conference on earthquake hazard reduction in the Central and Eastern United States: a time for examination and action. Earthquake Engineering Research Institute, Oakland, CA, pp 501–510
-
NZSEE (2017) The seismic assessment of existing buildings, Technical guidelines for engineering assessments, part A: assessment objectives and principles. Ministry of Business, Innovation and Employment. Earthquake Commission, New Zealand Society for Earthquake Engineering, Structural Engineering Society and New Zealand Geotechnical Society
-
Otani S (2004) Earthquake resistant design of reinforced concrete buildings: past and future. J Adv Concr Technol 2(1):3–24
Article Google Scholar
-
PEER (2017) Guidelines for performance-based seismic design of tall buildings. PEER report 2017/06. Pacific Earthquake Engineering Research Center, University of California, Berkeley, CA
-
Regione Autonoma Friuli-Venezia Giulia (1977) Raccomandazioni per la riparazione strutturale degli edifici in muratura. DT 2, Udine, Italy
-
Reitherman RK (2012) Earthquakes and engineers, An international history. ASCE, American Society of Civil Engineers, Reston
Book Google Scholar
-
Sorrentino L (2007) The early entrance of dynamics in earthquake engineering: Arturo Danusso's contribution. ISET J Earthq Technol 44(1):1–24
Google Scholar
-
Terzic V, Schoettler MJ, Restrepo JI, Mahin SA (2015) Concrete column blind prediction contest 2010: outcomes and observations. PEER Report 2015/01. Pacific Earthquake Engineering Research Center, Berkeley, CA
-
Tomaževič M (1978) Improvement of computer program POR. Report ZRMK-IK. Institute for Testing and Research in Materials and Structures, Ljubljana, Slovenia (in Slovenian)
-
Trifunac MD (2008) Early history of the response spectrum method, historical review. Soil Dyn Earthq Eng 28:676–685
Article Google Scholar
-
Whittaker A, Moehle J, Higashino M (1998) Evolution of seismic building design practice in Japan. Struct Des Tall Build 7:93–111
Article Google Scholar
-
Žižmond J, Dolšek M (2014) Risk-targeted seismic intensities and the behaviour factor for the force-based design of structures. University of Ljubljana, Faculty of Civil and Geodetic Engineering (Unpublished manuscript)
-
Žižmond J, Dolšek M (2017) The formulation of risk-targeted behaviour factor and its application to reinforced concrete buildings. In: Proceedings of the 16th world conference on earthquake engineering, Santiago, Chile, Paper No. 1659
Download references
Acknowledgements
The author is greatly indebted to the Awards Committee of the European Association for Earthquake Engineering, who granted him the Prof. Nicholas Ambraseys Distinguished Lecture Award. Much appreciation is expressed to the author's former PhD students who were involved in the development of the N2 method. Among them, Maja Kreslin, Damjan Marušić and Iztok Peruš greatly contributed to its extension. An important contribution to the development of the PRA approach was made by Mirko Kosič. He also helped with the technical editing of this paper. Great thanks go to the author's colleagues who kindly responded to a survey about the use of analysis methods in their own countries: Alireza Azarbakht, Mehmet Nuray Aydinoğlu, Ruben Boroschek, Rajesh Dhakal, Mohsen Ghafory-Ashtiany, Ron O. Hamburger, Jag Humar, Sudhir K. Jain, Masahiro Kurata, Koichi Kusunoki, Gregory MacRea, Roberto Meli, Eduardo Miranda, Khalid Mosalam, Taichiro Okazaki, Abdolreza Sarvghad-Moghadam, Haluk Sucuoğlu, and Keh-Chyuan Tsai. Very useful was the interaction with Edmund Booth and Michael N. Fardis. The perceptive comments of two reviewers, Matej Fischinger and Miha Tomaževič, are also much appreciated. The research work of the author and his colleagues has been continuously supported by the Slovenian Research Agency and its predecessors. This support is hereby gratefully acknowledged.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Reprints and Permissions
About this article
Cite this article
Fajfar, P. Analysis in seismic provisions for buildings: past, present and future. Bull Earthquake Eng 16, 2567–2608 (2018). https://doi.org/10.1007/s10518-017-0290-8
Download citation
-
Received:
-
Accepted:
-
Published:
-
Issue Date:
-
DOI : https://doi.org/10.1007/s10518-017-0290-8
Keywords
- Seismic codes
- Seismic analysis
- Dynamics
- Nonlinear analysis
- Pushover analysis
- Probability
- Seismic risk assessment
How Many Earthquake Records to Use for Design
Source: https://link.springer.com/article/10.1007/s10518-017-0290-8
0 Response to "How Many Earthquake Records to Use for Design"
Mag-post ng isang Komento